题目内容
AB是⊙O的直径,P是⊙O外一点,作PC⊥AB于C,PB交⊙O于D,DC交⊙O于E,EB与PC的延长线交于F,连接AE.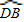 上有一动点M,连接PM,AM.
上有一动点M,连接PM,AM.(1)∠AEB的度数是______,根据是______.如果
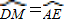 ,弦ED=3cm,⊙O的半径为2cm.则cos∠MAB=______.
,弦ED=3cm,⊙O的半径为2cm.则cos∠MAB=______.(2)求证:PC•CF=EC•CD.
(3)若AM交PC于G,△PGM满足什么条件时,PM与⊙O相切?说明理由.

【答案】分析:(1)根据直径所对的圆周角是直角;可得∠AEB=90°;根据余弦函数的定义可得cos∠MAB=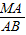 ,代入数据可得答案;
,代入数据可得答案;
(2)根据题意易得△ECF∽△PCD,可得比例关系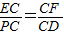 ,进而可得答案;
,进而可得答案;
(3)要使PM与⊙O相切,只需使OM⊥PM,根据角与角的关系可得当∠PGM=∠PMG或PG=PM时成立.
解答: (1)解:90°;直径所对的圆周角是直角;
(1)解:90°;直径所对的圆周角是直角; (3分)
(3分)
(2)证明:∵PC⊥AB,
∴∠CPD=90°-∠ABP=90°-∠AED又∠AEB=90°
∴∠CEF=90°-∠AED∴∠CPD=∠CEF(4分)
∵∠ECF=∠PCD
∴△ECF∽△PCD
∴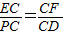
∴PC•CF=EC•CD(6分)
(3)解:∠PGM=∠PMG(PG=PM)时,PM与⊙O相切.(7分)
连接OM
∵PC⊥AB
∴∠BAM+∠AGC=90°
∵∠AGC=∠PGM=∠PMG
∵∠BAM=∠OMA
∴∠OMA+∠PMG=90°
即OM⊥PM,M在⊙O上
∴PM与⊙O相切.(10分)
点评:本题考查常见的几何题型,包括切线的判定、三角函数的定义与求法,要求学生掌握常见的解题方法,并能结合图形选择简单的方法解题.
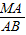 ,代入数据可得答案;
,代入数据可得答案;(2)根据题意易得△ECF∽△PCD,可得比例关系
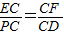 ,进而可得答案;
,进而可得答案;(3)要使PM与⊙O相切,只需使OM⊥PM,根据角与角的关系可得当∠PGM=∠PMG或PG=PM时成立.
解答:
 (1)解:90°;直径所对的圆周角是直角;
(1)解:90°;直径所对的圆周角是直角; (3分)
(3分)(2)证明:∵PC⊥AB,
∴∠CPD=90°-∠ABP=90°-∠AED又∠AEB=90°
∴∠CEF=90°-∠AED∴∠CPD=∠CEF(4分)
∵∠ECF=∠PCD
∴△ECF∽△PCD
∴
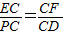
∴PC•CF=EC•CD(6分)
(3)解:∠PGM=∠PMG(PG=PM)时,PM与⊙O相切.(7分)
连接OM
∵PC⊥AB
∴∠BAM+∠AGC=90°
∵∠AGC=∠PGM=∠PMG
∵∠BAM=∠OMA
∴∠OMA+∠PMG=90°
即OM⊥PM,M在⊙O上
∴PM与⊙O相切.(10分)
点评:本题考查常见的几何题型,包括切线的判定、三角函数的定义与求法,要求学生掌握常见的解题方法,并能结合图形选择简单的方法解题.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=26,CD=24,求sin∠OCE的值.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=26,CD=24,求sin∠OCE的值. (1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP.
(1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP. (2012•大港区一模)如图,AB是⊙O的直径,C为圆上一点,∠BAC的平分线交于⊙O于点D,若∠ABC=40°,那么∠DBC的度数为( )
(2012•大港区一模)如图,AB是⊙O的直径,C为圆上一点,∠BAC的平分线交于⊙O于点D,若∠ABC=40°,那么∠DBC的度数为( ) 如图,已知AB是⊙O的直径,弦CD⊥AB,AC=3,BC=1,那么sin∠ABD的值是( )
如图,已知AB是⊙O的直径,弦CD⊥AB,AC=3,BC=1,那么sin∠ABD的值是( ) 如图,AB是半圆的直径,AB=2r,C、D为半圆的三等分点,则图中阴影部分的面积是( )
如图,AB是半圆的直径,AB=2r,C、D为半圆的三等分点,则图中阴影部分的面积是( )