题目内容
 如图所示,菱形ABCD中,∠A=120°,⊙O为△ABC外接圆,M为其上一点,连接MC交AB于E,AM交CB延长线于F.求证:D,E,F三点共线.
如图所示,菱形ABCD中,∠A=120°,⊙O为△ABC外接圆,M为其上一点,连接MC交AB于E,AM交CB延长线于F.求证:D,E,F三点共线.
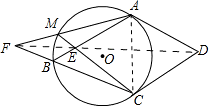 证明:如图,连AC,DF,DE.
证明:如图,连AC,DF,DE.因为M在⊙O上,
则∠AMC=60°=∠ABC=∠ACB,
有△AMC∽△ACF,得
 .
.又因为∠AMC=∠BAC,所以△AMC∽△EAC,得
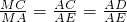 .
.所以
 ,又∠BAD=∠BCD=120°,知△CFD∽△ADE.
,又∠BAD=∠BCD=120°,知△CFD∽△ADE.所以∠ADE=∠DFB.因为AD∥BC,所以∠ADF=∠DFB=∠ADE,
于是F,E,D三点共线.
分析:连AC,DF,DE.∠AMC=60°=∠ABC=∠ACB,判定△AMC∽△ACF,利用对应边成比例再判定∠AMC=∠BAC,△AMC∽△EAC,又∠BAD=∠BCD=120°,知△CFD∽△ADE,∠ADE=∠DFB.因为AD∥BC,所以∠ADF=∠DFB=∠ADE,即可证明.
点评:此题考查学生对相似三角形的判定与性质和菱形的性质的理解和掌握,解题的关键是连AC,DF,DE.证明△AMC∽△ACF,△AMC∽△EAC,△CFD∽△ADE,这是此题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 23、如图所示,在△ABC中,AD⊥BC于点D,E,F分别是AB,AC边的中点,连接DE,EF,FD,当△ABC满足条件
23、如图所示,在△ABC中,AD⊥BC于点D,E,F分别是AB,AC边的中点,连接DE,EF,FD,当△ABC满足条件 30、如图所示,以△ABC的三边为边,分别作三个等边三角形.
30、如图所示,以△ABC的三边为边,分别作三个等边三角形. 已知:如图所示,在△ABC中,D、E、F分别是AB、BC、AC边上的中点.
已知:如图所示,在△ABC中,D、E、F分别是AB、BC、AC边上的中点.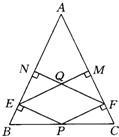 49、如图所示,在△ABC中,AB=AC,P为BC的中点,PE⊥AB于E,PF⊥AC于F,EM⊥AC于M,FN⊥AB于N,EM与FN相交于点Q,那么四边形PEQF是菱形吗?说明你的理由.
49、如图所示,在△ABC中,AB=AC,P为BC的中点,PE⊥AB于E,PF⊥AC于F,EM⊥AC于M,FN⊥AB于N,EM与FN相交于点Q,那么四边形PEQF是菱形吗?说明你的理由.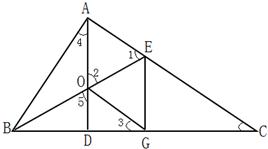 26、如图所示,Rt△ABC中,∠BAC=Rt∠,AD⊥BC于点D,∠ABC的平分线交AD于O,交AC于E,OG∥AC交BC于G.
26、如图所示,Rt△ABC中,∠BAC=Rt∠,AD⊥BC于点D,∠ABC的平分线交AD于O,交AC于E,OG∥AC交BC于G.