题目内容
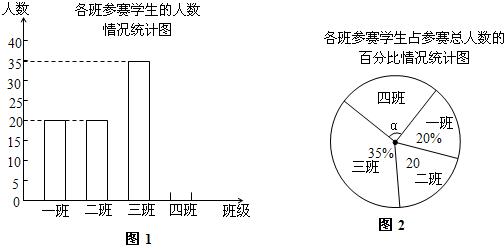
为了迎接建国六十周年,某中学九年级组织了《祖国在我心》征文比赛,共收到一班、二班、三班、四班参赛学生的文章共100篇(参赛学生每人只交了-篇),下面扇形统计图描述了各班参赛学生占总人数的百分比情况(尚不完整).比赛一、二等奖若干,结果全年级25人获奖,其中三班参赛学生的获奖率为20%,一、二、三、四班获奖人数的比为6:7:a: 5.
5.(1)填空:
①九(四)班有
②a=
(2)若获一等奖﹑二等奖的学生每人分别得到价值100元﹑60元的学习用品,购买这批奖品共用去1900元,问获一等奖﹑二等奖的学生人数分别是多少?
分析:(1)先求出九(四)班参赛人数,再用所占比例乘以360就得到α的度数.再根据一、二、三、四班获奖人数为6:7:a:5,求出a的值;得到各班获奖学生数的众数;
(2)设获一二等奖的学生人数分别为x人,y人,根据共有25人和共用去1900元,可以列方程组即可求得.
(2)设获一二等奖的学生人数分别为x人,y人,根据共有25人和共用去1900元,可以列方程组即可求得.
解答:解:(1)①九(四)班参赛人数有100×(1-20%-20%-35%)=25人;
α=360×(1-20%-20%-35%)=90度;
②三班参赛人数有100×35%=35,获奖者有35×20%=7,
因为一、二、三、四班获奖人数为6:7:a:5,所以a=7;
即一、二、三、四班获奖人数分别为6,7,7,5.
所以各班获奖学生数的众数是7;
(2)设获一二等奖的学生人数分别为x人,y人,则
,
解得:
.
即获一二等奖学生人数分别为10人,15人.
α=360×(1-20%-20%-35%)=90度;
②三班参赛人数有100×35%=35,获奖者有35×20%=7,
因为一、二、三、四班获奖人数为6:7:a:5,所以a=7;
即一、二、三、四班获奖人数分别为6,7,7,5.
所以各班获奖学生数的众数是7;
(2)设获一二等奖的学生人数分别为x人,y人,则
|
解得:
|
即获一二等奖学生人数分别为10人,15人.
点评:此题考查了学生的综合应用能力,解题的关键是掌握扇形图和方程组的应用以及众数的意义.

练习册系列答案
相关题目