题目内容
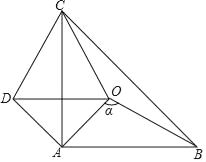
【题目】如图,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,点O是△ABC内的一点,∠BOC=130°.
(1)求证:OB=DC;
(2)求∠DCO的大小;
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.
【答案】(1)证明见解析;(2)40°;(3)当α的度数为115°或85°或145°时,△AOD是等腰三角形.
【解析】
(1)由已知证明△AOB≌△ADC,根据全等三角形的性质即可证得;
(2)由∠BOC=130°,根据周角的定义可得∠BOA+∠AOC=230°,再根据全等三角形的性质继而可得∠ADC+∠AOC=230°,由∠DAO=90°,在四边形AOCD中,根据四边形的内角和即可求得∠DCO的度数;
(3)分三种情况进行讨论即可得.
(1)∵∠BAC=∠OAD=90°,
∴∠BAC﹣∠CAO=∠OAD﹣∠CAO,
∴∠DAC=∠OAB,
在△AOB与△ADC中,
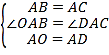 ,
,
∴△AOB≌△ADC,
∴OB=DC;
(2)∵∠BOC=130°,
∴∠BOA+∠AOC=360°﹣130°=230°,
∵△AOB≌△ADC
∠AOB=∠ADC,
∴∠ADC+∠AOC=230°,
又∵△AOD是等腰直角三角形,
∴∠DAO=90°,
∴四边形AOCD中,∠DCO=360°﹣90°﹣230°=40°;
(3)当CD=CO时,
∴∠CDO=∠COD=![]() =70°,
=70°,
∵△AOD是等腰直角三角形,
∴∠ODA=45°,
∴∠CDA=∠CDO+∠ODA=70°+45°=115°,
又∠AOB=∠ADC=α,
∴α=115°;
当OD=CO时,
∴∠DCO=∠CDO=40°,
∴∠CDA=∠CDO+∠ODA=40°+45°=85°,
∴α=85°;
当CD=OD时,
∴∠DCO=∠DOC=40°,
∠CDO=180°﹣∠DCO﹣∠DOC=180°﹣40°﹣40°=100°,
∴∠CDA=∠CDO+∠ODA=100°+45°=145°,
∴α=145°,
综上所述:当α的度数为115°或85°或145°时,△AOD是等腰三角形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在水果销售旺季,某水果店购进一优质水果,进价为 20 元/千克,售价不低于 20 元/千克,且不超过 32 元/千克,根据销售情况,发现该水果一天的销售量 y(千克)与该天的售价 x(元/千克)满足如下表所示的一次函数关系.
销售量 y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价 x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为 23.5 元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利 150 元,那么该天水果的售价为多少元?