题目内容
【题目】如图,平面直角坐标系中,O为坐标原点,正方形OABC的定点A,B都在反比例函数y=![]() (k>0,x>0)的图象上,边BC与x轴交于点D,则
(k>0,x>0)的图象上,边BC与x轴交于点D,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
过A作AE⊥x轴于E,过B作BF⊥x轴于F,BG⊥AE于G,于是得到EF=BG,BF=GE,根据正方形的性质得到OA=AB,∠OAB=90°,根据余角的性质得到∠OAE=∠ABG,根据全等三角形的性质得到AG=OE,AE=BG,设A(a,![]() ),得到OE=AG=a,AE=BG=
),得到OE=AG=a,AE=BG=![]() ,求得B(
,求得B(![]() +a,
+a,![]() -a),得方程求得k=
-a),得方程求得k=![]() a2(负值舍去),过C作CH⊥x轴于H,根据相似三角形的性质即可得到结论.
a2(负值舍去),过C作CH⊥x轴于H,根据相似三角形的性质即可得到结论.
解:过A作AE⊥x轴于E,过B作BF⊥x轴于F,BG⊥AE于G,
则EF=BG,BF=GE,
∵四边形OABC是正方形,
∴OA=AB,∠OAB=90°,
∴∠OAE+∠BAE=∠BAE+∠ABG=90°,
∴∠OAE=∠ABG,
在△AOE与△BAG中,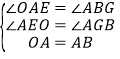 ,
,
∴△AOE≌△BAG,
∴AG=OE,AE=BG,
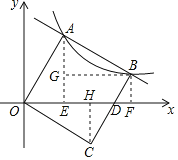
设A(a,![]() ),
),
∴OE=AG=a,AE=BG=![]() ,
,
∴B(![]() +a,
+a,![]() -a),
-a),
∴(![]() +a)(
+a)(![]() -a)=k,
-a)=k,
解得k=![]() a2(负值舍去),
a2(负值舍去),
∴B点的纵坐标为![]() a,
a,
BF=![]() a,
a,
过C作CH⊥x轴于H,
同理△AOE≌△OCH,
∴CH=OE=a,
∵CH⊥x轴,BF⊥x轴,
∴CH∥BF,
∴△BFD∽△CHD,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
故选:D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】光明中学全体学生900人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
![]() 填写下表:
填写下表:
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩 |
![]() 估计光明中学全体学生社会实践活动成绩的总分.
估计光明中学全体学生社会实践活动成绩的总分.