题目内容
 如图,半圆D的直径AB=4,与半圆O内切的动圆O1与AB切于点M,设⊙O1的半径为y,AM=x,则y关于x的函数关系式是
如图,半圆D的直径AB=4,与半圆O内切的动圆O1与AB切于点M,设⊙O1的半径为y,AM=x,则y关于x的函数关系式是
- A.y=-
 x2+x
x2+x - B.y=-x2+x
- C.y=-
 x2-x
x2-x - D.y=
 x2-x
x2-x
A
分析:连接01M,OO1,可得到直角三角形OO1M,在直角三角形中,利用勾股定理即可解得.
解答: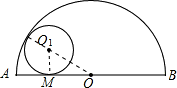 解:连接01M,OO1,可得到直角三角形OO1M,
解:连接01M,OO1,可得到直角三角形OO1M,
依题意可知⊙O的半径为2,
则OO1=2-y,OM=2-x,O1M=y.
在Rt△OO1M中,由勾股定理得(2-y)2-(2-x)2=y2,
解得y=- x2+x.
x2+x.
故选A.
点评:作连心线,连接圆心和切点得到直角三角形是常用的辅助线作法是本题的考查对象.
分析:连接01M,OO1,可得到直角三角形OO1M,在直角三角形中,利用勾股定理即可解得.
解答:
 解:连接01M,OO1,可得到直角三角形OO1M,
解:连接01M,OO1,可得到直角三角形OO1M,依题意可知⊙O的半径为2,
则OO1=2-y,OM=2-x,O1M=y.
在Rt△OO1M中,由勾股定理得(2-y)2-(2-x)2=y2,
解得y=-
 x2+x.
x2+x.故选A.
点评:作连心线,连接圆心和切点得到直角三角形是常用的辅助线作法是本题的考查对象.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
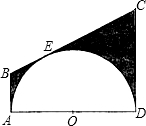 如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.
如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.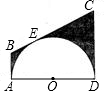 如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
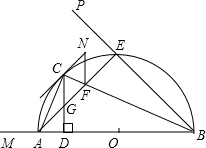 N∥CD,过C作圆的切线交FN于N.
N∥CD,过C作圆的切线交FN于N. 如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( )
如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( ) 如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.
如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.