题目内容
若a,b,c为三角形三边,则关于的二次方程 x2+(a-b)x+c2=0的根的情况是
x2+(a-b)x+c2=0的根的情况是
- A.有两个相等的实数根
- B.有两个不相等的实数根
- C.没有实数根
- D.无法确定
C
分析:先求出△=b2-4ac,再结合a,b,c为三角形的三边,即可判断根的情况.
解答:∵ x2+(a-b)x+c2=0,
x2+(a-b)x+c2=0,
∴△=b2-4ac=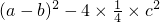 =(a-b)2-c2=(a-b-c)(a-b+c)
=(a-b)2-c2=(a-b-c)(a-b+c)
∵a,b,c为三角形三边,
∴b+c>a,a+c>b
∴a-b-c<0,a-b+c>0
∴(a-b-c)(a-b+c)<0,
即二次方程 x2+(a-b)x+c2=0无实数根.
x2+(a-b)x+c2=0无实数根.
故选C.
点评:本题考查了一元二次方程根的判别式的应用及三角形三边的关系.
分析:先求出△=b2-4ac,再结合a,b,c为三角形的三边,即可判断根的情况.
解答:∵
 x2+(a-b)x+c2=0,
x2+(a-b)x+c2=0,∴△=b2-4ac=
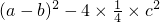 =(a-b)2-c2=(a-b-c)(a-b+c)
=(a-b)2-c2=(a-b-c)(a-b+c)∵a,b,c为三角形三边,
∴b+c>a,a+c>b
∴a-b-c<0,a-b+c>0
∴(a-b-c)(a-b+c)<0,
即二次方程
 x2+(a-b)x+c2=0无实数根.
x2+(a-b)x+c2=0无实数根.故选C.
点评:本题考查了一元二次方程根的判别式的应用及三角形三边的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若a、b、c为三角形三边长,则下列各项中不能构成直角三角形的是( )
| A、a=6,b=8,c=10 | ||
| B、a=7,b=24,c=25 | ||
| C、a=1,b=2,c=3 | ||
D、a=n,b=
|