题目内容
 如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=
如图,已知E、F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=| 2 |
| 3 |
| A、5个 | B、4个 | C、3个 | D、2个 |
考点:正方形的性质,全等三角形的判定与性质
专题:压轴题
分析:根据正方形的性质可得AB=BC=AD,∠ABC=∠BAD=90°,再根据中点定义求出AE=BF,然后利用“边角边”证明△ABF和△DAE全等,根据全等三角形对应角相等可得∠BAF=∠ADE,然后求出∠ADE+∠DAF=∠BAD=90°,从而求出∠AMD=90°,再根据邻补角的定义可得∠AME=90°,从而判断①正确;根据中线的定义判断出∠ADE≠∠EDB,然后求出∠BAF≠∠EDB,判断出②错误;根据直角三角形的性质判断出△AED、△MAD、△MEA三个三角形相似,利用相似三角形对应边成比例可得
=
=
=2,然后求出MD=2AM=4EM,判断出④正确,设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据相似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM=
MF,判断出⑤正确;过点M作MN⊥AB于N,求出MN、NB,然后利用勾股定理列式求出BM,过点M作GH∥AB,过点O作OK⊥GH于K,然后求出OK、MK,再利用勾股定理列式求出MO,根据正方形的性质求出BO,然后利用勾股定理逆定理判断出∠BMO=90°,从而判断出③正确.
| AM |
| EM |
| MD |
| AM |
| AD |
| AE |
| 2 |
| 3 |
解答:解:在正方形ABCD中,AB=BC=AD,∠ABC=∠BAD=90°,
∵E、F分别为边AB,BC的中点,
∴AE=BF=
BC,
在△ABF和△DAE中,
,
∴△ABF≌△DAE(SAS),
∴∠BAF=∠ADE,
∵∠BAF+∠DAF=∠BAD=90°,
∴∠ADE+∠DAF=∠BAD=90°,
∴∠AMD=180°-(∠ADE+∠DAF)=180°-90°=90°,
∴∠AME=180°-∠AMD=180°-90°=90°,故①正确;
∵DE是△ABD的中线,
∴∠ADE≠∠EDB,
∴∠BAF≠∠EDB,故②错误;
∵∠BAD=90°,AM⊥DE,
∴△AED∽△MAD∽△MEA,
∴
=
=
=2,
∴AM=2EM,MD=2AM,
∴MD=2AM=4EM,故④正确;
设正方形ABCD的边长为2a,则BF=a,
在Rt△ABF中,AF=
=
=
a,
∵∠BAF=∠MAE,∠ABC=∠AME=90°,
∴△AME∽△ABF,
∴
=
,
即
=
,
解得AM=
a,
∴MF=AF-AM=
a-
a=
a,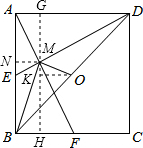
∴AM=
MF,故⑤正确;
如图,过点M作MN⊥AB于N,
则
=
=
,
即
=
=
,
解得MN=
a,AN=
a,
∴NB=AB-AN=2a-
a=
a,
根据勾股定理,BM=
=
=
a,
过点M作GH∥AB,过点O作OK⊥GH于K,
则OK=a-
a=
a,MK=
a-a=
a,
在Rt△MKO中,MO=
=
=
a,
根据正方形的性质,BO=2a×
=
a,
∵BM2+MO2=(
a)2+(
a)2=2a2,
BO2=(
a)2=2a2,
∴BM2+MO2=BO2,
∴△BMO是直角三角形,∠BMO=90°,故③正确;
综上所述,正确的结论有①③④⑤共4个.
故选B.
∵E、F分别为边AB,BC的中点,
∴AE=BF=
| 1 |
| 2 |
在△ABF和△DAE中,
|
∴△ABF≌△DAE(SAS),
∴∠BAF=∠ADE,
∵∠BAF+∠DAF=∠BAD=90°,
∴∠ADE+∠DAF=∠BAD=90°,
∴∠AMD=180°-(∠ADE+∠DAF)=180°-90°=90°,
∴∠AME=180°-∠AMD=180°-90°=90°,故①正确;
∵DE是△ABD的中线,
∴∠ADE≠∠EDB,
∴∠BAF≠∠EDB,故②错误;
∵∠BAD=90°,AM⊥DE,
∴△AED∽△MAD∽△MEA,
∴
| AM |
| EM |
| MD |
| AM |
| AD |
| AE |
∴AM=2EM,MD=2AM,
∴MD=2AM=4EM,故④正确;
设正方形ABCD的边长为2a,则BF=a,
在Rt△ABF中,AF=
| AB2+BF2 |
| (2a)2+a2 |
| 5 |
∵∠BAF=∠MAE,∠ABC=∠AME=90°,
∴△AME∽△ABF,
∴
| AM |
| AB |
| AE |
| AF |
即
| AM |
| 2a |
| a | ||
|
解得AM=
2
| ||
| 5 |
∴MF=AF-AM=
| 5 |
2
| ||
| 5 |
3
| ||
| 5 |

∴AM=
| 2 |
| 3 |
如图,过点M作MN⊥AB于N,
则
| MN |
| BF |
| AN |
| AB |
| AM |
| AF |
即
| MN |
| a |
| AN |
| 2a |
| ||||
|
解得MN=
| 2 |
| 5 |
| 4 |
| 5 |
∴NB=AB-AN=2a-
| 4 |
| 5 |
| 6 |
| 5 |
根据勾股定理,BM=
| NB2+MN2 |
(
|
2
| ||
| 5 |
过点M作GH∥AB,过点O作OK⊥GH于K,
则OK=a-
| 2 |
| 5 |
| 3 |
| 5 |
| 6 |
| 5 |
| 1 |
| 5 |
在Rt△MKO中,MO=
| MK2+OK2 |
(
|
| ||
| 5 |
根据正方形的性质,BO=2a×
| ||
| 2 |
| 2 |
∵BM2+MO2=(
2
| ||
| 5 |
| ||
| 5 |
BO2=(
| 2 |
∴BM2+MO2=BO2,
∴△BMO是直角三角形,∠BMO=90°,故③正确;
综上所述,正确的结论有①③④⑤共4个.
故选B.
点评:本题考查了正方形的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理的应用,勾股定理逆定理的应用,综合性较强,难度较大,仔细分析图形并作出辅助线构造出直角三角形与相似三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若a<b,則下列不等式正確的是( )
| A、a-2<b-2 | ||||
| B、a-b>0 | ||||
C、
| ||||
| D、-2a<-2b |
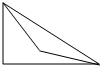 如图直角三角形两锐角的角平分线所交成的角的度数是( )
如图直角三角形两锐角的角平分线所交成的角的度数是( )| A、115° | B、135° |
| C、120° | D、都不对 |
 如图,直线y=
如图,直线y=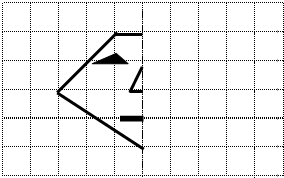 如图是人头像的一半,以图中虚线为对称轴画出它的另一半.
如图是人头像的一半,以图中虚线为对称轴画出它的另一半.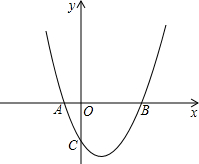 如图,抛物线y=x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C.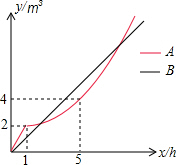 A、B两个水管同时开始向一个空容器内注水.如图是A、B两个水管各自注水量y(m3)与注水时间x(h)之间的函数图象,已知B水管的注水速度是1m3/h,1小时后,A水管的注水量随时间的变化是一段抛物线,其顶点是(1,2),且注水9小时,容器刚好注满.请根据图象所提供的信息解答下列问题:
A、B两个水管同时开始向一个空容器内注水.如图是A、B两个水管各自注水量y(m3)与注水时间x(h)之间的函数图象,已知B水管的注水速度是1m3/h,1小时后,A水管的注水量随时间的变化是一段抛物线,其顶点是(1,2),且注水9小时,容器刚好注满.请根据图象所提供的信息解答下列问题: