��Ŀ����
����Ŀ����ͼ1����֪��ABC�ǵ���ֱ�������Σ���BAC=90�㣬��D��BC���е㣮��������DEFG��ʹ��A��C�ֱ���DG��DE�ϣ�����AE��BG��
��1����֤��AE=BG
��2����������DEFG�Ƶ�D��ʱ�뷽����ת����0�㣼����360�㣩��ͼ2��ʾ���жϣ�1���еĽ����Ƿ���Ȼ����������Գ����������֤�����������������˵�����ɣ�
��3����BC=DE=4������ת�Ǧ�Ϊ���ٶ�ʱ��AEȡ�����ֵ��ֱ��д��AEȡ�����ֵʱ���Ķ����������ñ���ͼ������ʱ��������DEFG����������ʱAF��ֵ��
���𰸡�
��1��
֤�����ߡ�ABC�ǵ���ֱ�������Σ���BAC=90�㣬��D��BC���е㣬
��AD��BC��BD=CD��
���ADB=��ADC=90�㣬AD=DC=DB��
���ı���DEFG�������Σ�
��DE=DG��
���ADE�ա�BDG��SAS����
��BG=AE��
��2��
�⣺������
�������£���ͼ2������AD��
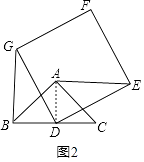
�ɣ�1��֪AD=BD��AD��BC��
���ADG+��GDB=90�㣮
���ı���EFGDΪ�����Σ�
��DE=DG���ҡ�GDE=90�㣮
���ADG+��ADE=90��
���BDG=��ADE��
�ڡ�BDG�͡�ADE�У�
��BD=AD����BDG=��ADE��GD=ED��
���BDG�ա�ADE��SAS��
��AE=BG��
��3��
�⣺��=270�㣻
������DEFG��ͼ3��ʾ
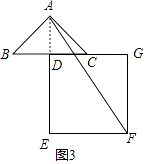
�ɣ�2��֪BG=AE
�൱BGȡ�����ֵʱ��AEȡ�����ֵ��
��BC=DE=4��
��EF=4��
��BG=2+4=6
��AE=6
��Rt��AEF�У��ɹ��ɶ�������
AF= ![]() =
= ![]() =2
=2 ![]() ��
��
����������1����Rt��BDG��Rt��EDA�����ݱ߽DZ߶�����Rt��BDG��Rt��EDA����BG=AE����2������AD������ֱ���������������ε����ʿɵ�Rt��BDG��Rt��EDA�������ɵ�BG=AE����3�����ݣ�2���Ľ��ۣ���BG�����ֵ�������ɵô�ʱF��λ�ã��ɹ��ɶ����ɵô𰸣�
�����㾫����������Ŀ����֪���������õ���ֱ�������κ��ɶ����ĸ�������֪ʶ���Եõ�����Ĵ𰸣���Ҫ���յ���ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��

 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д�