题目内容
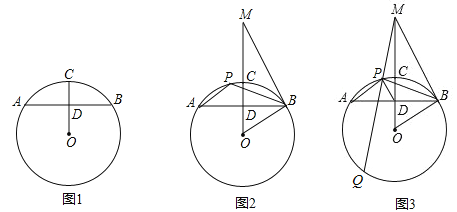
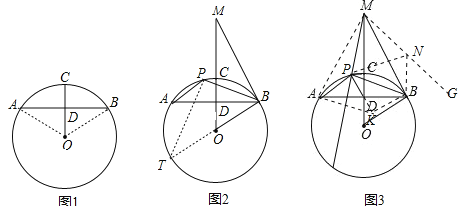
【题目】(2017黑龙江省哈尔滨市,第26题,10分)已知:AB是⊙O的弦,点C是![]() 的中点,连接OB、OC,OC交AB于点D.
的中点,连接OB、OC,OC交AB于点D.
(1)如图1,求证:AD=BD;
(2)如图2,过点B作⊙O的切线交OC的延长线于点M,点P是![]() 上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°;
上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°;
(3)如图3,在(2)的条件下,连接DP、MP,延长MP交⊙O于点Q,若MQ=6DP,sin∠ABO=![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)如图1,连接OA,利用垂径定理和圆周角定理可得结论;
(2)如图2,延长BO交⊙O于点T,连接PT,由圆周角定理可得∠BPT=90°,易得∠APT=∠APB﹣∠BPT=∠APB﹣90°,利用切线的性质定理和垂径定理可得∠ABO=∠OMB,等量代换可得∠ABO=∠APT,易得结论;
(3)如图3,连接MA,利用垂直平分线的性质可得MA=MB,易得∠MAB=∠MBA,作∠PMG=∠AMB,在射线MG上截取MN=MP,连接PN,BN,易得△APM≌△BNM,由全等三角形的性质可得AP=BN,∠MAP=∠MBN,延长PD至点K,使DK=DP,连接AK、BK,易得四边形APBK是平行四边形,由平行四边形的性质和平行线的性质可得∠PAB=∠ABK,∠APB+∠PBK=180°,由(2)得∠APB﹣(90°﹣∠MBA)=90°,易得∠NBP=∠KBP,可得△PBN≌△PBK,PN=2PH,利用三角函数的定义可得sin∠PMH=![]() ,sin∠ABO=
,sin∠ABO=![]() ,设DP=3a,则PM=5a,可得结果.
,设DP=3a,则PM=5a,可得结果.
(1)如图1,连接OA,
∵C是![]() 的中点,
的中点,
∴![]() ,
,
∴∠AOC=∠BOC,
∵OA=OB,
∴OD⊥AB,AD=BD;
(2)如图2,延长BO交⊙O于点T,连接PT.
∵BT是⊙O的直径,
∴∠BPT=90°,
∴∠APT=∠APB﹣∠BPT=∠APB﹣90°,
∵BM是⊙O的切线,
∴OB⊥BM,
又∵∠OBA+∠MBA=90°,
∴∠ABO=∠OMB.
又∵∠ABO=∠APT,
∴∠APB﹣90°=∠OMB,
∴∠APB﹣∠OMB=90°;
(3)如图3,连接MA,
∵MO垂直平分AB,∴MA=MB,
∴∠MAB=∠MBA,
作∠PMG=∠AMB,在射线MG上截取MN=MP,连接PN,BN,则∠AMP=∠BMN,
∴△APM≌△BNM,
∴AP=BN,∠MAP=∠MBN,延长PD至点K,使DK=DP,连接AK、BK,
∴四边形APBK是平行四边形;
∵AP∥BK,
∴∠PAB=∠ABK,∠APB+∠PBK=180°,
由(2)得∠APB﹣(90°﹣∠MBA)=90°,
∴∠APB+∠MBA=180°,∴∠PBK=∠MBA,
∴∠MBP=∠ABK=∠PAB,
∴∠MAP=∠PBA=∠MBN,
∴∠NBP=∠KBP,∵PB=PB,
∴△PBN≌△PBK,
∴PN=PK=2PD,过点M作MH⊥PN于点H,
∴PN=2PH,∴PH=DP,∠PMH=∠ABO,
∵sin∠PMH=![]() ,sin∠ABO=
,sin∠ABO=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,设DP=3a,则PM=5a,∴MQ=6DP=18a,
,设DP=3a,则PM=5a,∴MQ=6DP=18a,
∴![]() =
=![]() .
.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案【题目】为了了解某区九年级数学教学质量检测情况,进行了抽样调查,其过程如下,请补全表一、表二中的空白,并回答提出的问题.
收集数据:随机抽取甲、乙两所学校中各自取20名学生的数学成绩进行分析
甲:91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91
乙:84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88
整理数据:表一
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 | 0 | 0 | 1 | 2 | 8 | 5 |
分析数据:表二
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 | 88 | 91 | 268.43 |
乙 | 81.95 | 86 | 115.25 |
得出结论:
(1)若甲学校有400名九年级学生,估计这次考试成绩80分(包含80分)以上人数为 .
(2)可以推断出 (填:甲或乙)学校学生的数学水平较高,理由是 (至少从两个不同角度说明推断的合理性).
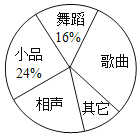
【题目】某校为了庆祝建国七十周年,决定举办一台文艺晚会,为了了解学生最喜爱的节目形式,随机抽取了部分学生进行调查,规定每人从“歌曲”,“舞蹈”,“小品”,“相声”和“其它”五个选项中选择一个,并将调查结果绘制成如下两幅不完整的统计图表,请根据图中信息,解答下列题:
最喜爱的节目 | 人数 |
歌曲 | 15 |
舞蹈 | a |
小品 | 12 |
相声 | 10 |
其它 | b |
(1)在此次调查中,该校一共调查了 名学生;
(2)a= ;b= ;
(3)在扇形计图中,计算“歌曲”所在扇形的圆心角的度数;
(4)若该校共有1200名学生,请你估计最喜爱“相声”的学生的人数.
【题目】我市某初中课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
182 | 195 | 201 | 179 | 208 | 204 | 186 | 192 | 210 | 204 |
175 | 193 | 200 | 203 | 188 | 197 | 212 | 207 | 185 | 206 |
188 | 186 | 198 | 202 | 221 | 199 | 219 | 208 | 187 | 224 |
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
谷粒颗数 | 175≤x<185 | 185≤x<195 | 195≤x<205 | 205≤x<215 | 215≤x<225 |
频数 | 8 | 10 | 3 | ||
对应扇形 图中区域 | D | E | C |

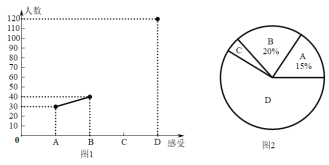
(2)如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(3)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?