题目内容
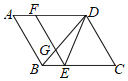
【题目】如图,菱形ABCD中,AB=3,E是BC上一个动点(不与点B、C重合),EF∥AB,交BD于点G,设BE=x,△GED的面积与菱形ABCD的面积之比为y,则y与x的函数图象大致为( )
A. B.
B.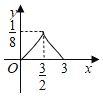 C.
C.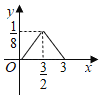 D.
D.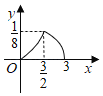
【答案】A
【解析】
连接BF,求出平行四边形ABEF与平行四边形ABCD的面积关系,再求得△BEF与△BEF的面积关系,进而得△BDE与平行四边形ABCD的面积的关系,再证明△GBE∽△GDF,得出GE:GF,进而得△BEG与△BEF的面积关系,最后得y与x的关系式,根据函数关系式确定函数图象.
解:连接BF,

∵四边形ABCD是菱形,AB=3,
∴AD∥BC,AB=BC=CD=AD=3,
∵EF∥AB,
∴四边形ABEF是平行四边形,
∴AF=BE=x,
∴![]() =,
=,
∵AD∥BC,
∴△GBE∽△GDF,
∴![]() ,
,
∴![]() ,
,
∵AD∥BC,
∴![]() ,
,
∴S△GED=S△BED﹣S△BEG=![]() =
=![]() ,
,
∴![]() ,
,
即y=![]() (0<x<3),
(0<x<3),
∵![]() ,
,
∴y=![]() (0<x<3)是开口向下的抛物线,
(0<x<3)是开口向下的抛物线,
故选:A.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目