Question

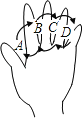
【题目】如图，在各个手指间标记字母A，B，C，D．请你按图中箭头所指方向（即ABCDCBABC…的方式）从A开始数连续的正整数1，2，3，4…当数到11时，对应的字母是__．当字母C第2n﹣1次出现时（n为正整数），恰好数到的数是__（用含n的代数式表示）．

Answer 1

【答案】C 3（2n﹣1）．

【解析】

根据数字的变化发现规律字母C第1次出现时，恰好数到的数是3=1×3，字母C第3次出现时，恰好数到的数是9=3×3，…，字母C第2n-1次出现时（n为正整数），恰好数到的数是3（2n-1）．即可得结论．

解：根据题意，得

从A开始数连续的正整数1，2，3，4…当数到11时，对应的字母是C．

当ABCDCBABC…

字母C第1次出现时，恰好数到的数是3＝1×3，

字母C第2次出现时，恰好数到的数是5＝2×3﹣1，

字母C第3次出现时，恰好数到的数是，9＝3×3，

字母C第4次出现时，恰好数到的数是11＝4×3﹣1，

…

发现规律

字母C第2n﹣1次出现时（n为正整数），恰好数到的数是3（2n﹣1）．

故答案为：C；3（2n﹣1）．