题目内容
【题目】如图，AB∥DE，AC∥DF，AC＝DF，添加下列条件，不能判断 △ABC≌△DEF的是（ ）
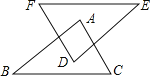
A. EF＝BC B. AB＝DE C. EF∥BC D. 
B＝E
【答案】A
【解析】
根据全等三角形的判定方法结合所给条件逐项分析即可.
∵AB∥DE,
∴∠1=∠2.
∵AC∥DF,
∴∠1=∠D,
∴∠2=∠D.
A. 在△ABC和△DEF中，
AC＝DF，
EF＝BC，
∠2=∠D，
此3个条件符合“SSA”，而“SSA”不能作为全等三角形的判定方法，故A不能判断 △ABC≌△DEF；
B. 在△ABC和△DEF中，
AC＝DF，
∠2=∠D，
AB＝DE，
∴△ABC≌△DEF（SAS），
故B能判断 △ABC≌△DEF；
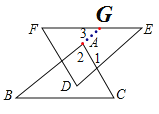
C.延长BA交FE于点G.
∵EF∥BC,
∴∠3=∠B.
∵AB∥DE,
∴∠3=∠E,
∴∠B=∠E.
在△ABC和△DEF中，
∠B=∠E，
∠2=∠D，
AC＝DF，
∴△ABC≌△DEF（AAS），
故C能判断 △ABC≌△DEF；
D. 在△ABC和△DEF中，
∠B=∠E，
∠2=∠D，
AC＝DF，
∴△ABC≌△DEF（AAS），
故D能判断 △ABC≌△DEF；
故选A.
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
