题目内容
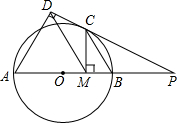 如图,已知AB是⊙O的直径,PC切⊙O于C,AD⊥PD,CM⊥AB,垂足分别为D,M.
如图,已知AB是⊙O的直径,PC切⊙O于C,AD⊥PD,CM⊥AB,垂足分别为D,M.(1)求证:CB平分∠PCM;
(2)若∠CBA=60°,求证:△ADM为等边三角形;
(3)若PO=5,PC=a,⊙O的半径为r,且a,r是关于x的方程x2-(2m+1)x+4m=0的两根,求m的值.
分析:(1)延长CM与圆相交于E,连接OC,OE,根据垂径定理,
=
,根据弦切角定理即可解答.
(2)根据已知及等边三角形的判定方法证明即可.
(3)先根据勾股定理找出PO=5,PC=a,⊙O的半径r之间的关系,再利用一元二次方程根与系数的关系可直接解答.
 |
| CB |
 |
| BE |
(2)根据已知及等边三角形的判定方法证明即可.
(3)先根据勾股定理找出PO=5,PC=a,⊙O的半径r之间的关系,再利用一元二次方程根与系数的关系可直接解答.
解答: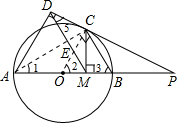 (1)证明:延长CM与圆相交于E,连接OC,OE;
(1)证明:延长CM与圆相交于E,连接OC,OE;
∵CM⊥AB,
∴
=
.
∴∠COP=∠EOP.
∴∠BCP=
∠COP,∠MCB=
∠EOP.
∴∠BCP=∠MCB,CB平分∠PCM.
(2)证明:∵∠CBA=60°,
∴∠1=∠ACD=30°.
∵∠COB是△AOC的外角,
∴∠COB=60°.
又∵AD⊥PC,OC⊥PC,
∴AD∥OC,∠DAM=∠COB=60°.
∵△BOC是等边三角形,CM⊥OB,
∴∠BCM=30°.
∵CB平分∠PCM,
∴∠PCB=30°.
∴∠1=∠PCB=30°.
又∵∠DAM=60°,
∴∠DAC=∠1=30°.
∴AC是∠DAM的平分线.
∵∠ADC=∠CMA=90°,
∴CD=CM,△ADC≌△AMC,AD=AM.
∴∠ADM=∠AMD.
又∵∠DAM=60°,
∴∠DAM=∠ADM=∠AMD=60°.
即△ADM为等边三角形;
(3)解:∵PO=5,PC=a,⊙O的半径为r,
∴在Rt△OCP中,OC2+PC2=OP2
即r2+a2=52①
∵a,r是关于x的方程x2-(2m+1)x+4m=0的两根
∴a+r=2m+1,ar=4m ②
∴(a+r)2=a2+r2+2ar ③
把①②代入③得(2m+1)2=25+8m,解得m=3或m=-2(舍去)
故m=3.
 (1)证明:延长CM与圆相交于E,连接OC,OE;
(1)证明:延长CM与圆相交于E,连接OC,OE;∵CM⊥AB,
∴
 |
| CB |
 |
| BE |
∴∠COP=∠EOP.
∴∠BCP=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BCP=∠MCB,CB平分∠PCM.
(2)证明:∵∠CBA=60°,
∴∠1=∠ACD=30°.
∵∠COB是△AOC的外角,
∴∠COB=60°.
又∵AD⊥PC,OC⊥PC,
∴AD∥OC,∠DAM=∠COB=60°.
∵△BOC是等边三角形,CM⊥OB,
∴∠BCM=30°.
∵CB平分∠PCM,
∴∠PCB=30°.
∴∠1=∠PCB=30°.
又∵∠DAM=60°,
∴∠DAC=∠1=30°.
∴AC是∠DAM的平分线.
∵∠ADC=∠CMA=90°,
∴CD=CM,△ADC≌△AMC,AD=AM.
∴∠ADM=∠AMD.
又∵∠DAM=60°,
∴∠DAM=∠ADM=∠AMD=60°.
即△ADM为等边三角形;
(3)解:∵PO=5,PC=a,⊙O的半径为r,
∴在Rt△OCP中,OC2+PC2=OP2
即r2+a2=52①
∵a,r是关于x的方程x2-(2m+1)x+4m=0的两根
∴a+r=2m+1,ar=4m ②
∴(a+r)2=a2+r2+2ar ③
把①②代入③得(2m+1)2=25+8m,解得m=3或m=-2(舍去)
故m=3.
点评:此题考查的是圆的有关知识与一元二次方程根与系数的关系相结合,难度比较大,需同学们细心解答.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10.
如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10. 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F. (2013•泰安)如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是
(2013•泰安)如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是 如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC.
如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC. 如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.
如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.