Question

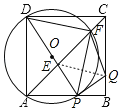
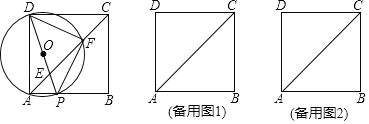
【题目】如图，在正方形ABCD中，AB＝4，动点P从点A出发，以每秒2个单位的速度，沿线段AB方向匀速运动，到达点B停止．连接DP交AC于点E，以DP为直径作⊙O交AC于点F，连接DF、PF．

（1）求证：△DPF为等腰直角三角形；

（2）若点P的运动时间t秒．

①当t为何值时，点E恰好为AC的一个三等分点；

②将△EFP沿PF翻折，得到△QFP，当点Q恰好落在BC上时，求t的值．

Answer 1

【答案】（1）详见解析；（2）①1；②﹣1．

【解析】

（1）要证明三角形△DPF为等腰直角三角形，只要证明∠DFP＝90°，∠DPF＝∠PDF＝45°即可，根据直径所对的圆周角是90°和同弧所对的圆周角相等，可以证明∠DFP＝90°，∠DPF＝∠PDF＝45°，从而可以证明结论成立；

（2）①根据题意，可知分两种情况，然后利用分类讨论的方法，分别计算出相应的t的值即可，注意点P从A出发到B停止，t≤4÷2＝2；

②根据题意，画出相应的图形，然后利用三角形相似，勾股定理，即可求得t的值．

证明：（1）∵四边形ABCD是正方形，AC是对角线，

∴∠DAC＝45°，

∵在⊙O中，所对的圆周角是∠DAF和∠DPF，

∴∠DAF＝∠DPF，

∴∠DPF＝45°，

又∵DP是⊙O的直径，

∴∠DFP＝90°，

∴∠FDP＝∠DPF＝45°，

∴△DFP是等腰直角三角形；

（2）①当AE：EC＝1：2时，

∵AB∥CD，

∴∠DCE＝∠PAE，∠CDE＝∠APE，

∴△DCE∽△PAE，

∴，

∴，

解得，t＝1；

当AE：EC＝2：1时，

∵AB∥CD，

∴∠DCE＝∠PAE，∠CDE＝∠APE，

∴△DCE∽△PAE，

∴，

∴，

解得，t＝4，

∵点P从点A到B，t的最大值是4÷2＝2，

∴当t＝4时不合题意，舍去；

由上可得，当t为1时，点E恰好为AC的一个三等分点；

②如右图所示，

∵∠DPF＝90°，∠DPF＝∠OPF，

∴∠OPF＝90°，

∴∠DPA+∠QPB＝90°，

∵∠DPA+∠PDA＝90°，

∴∠PDA＝∠QPB，

∵点Q落在BC上，

∴∠DAP＝∠B＝90°，

∴△DAP∽△PBQ，

∴，

∵DA＝AB＝4，AP＝2t，∠DAP＝90°，

∴DP＝＝2，PB＝4﹣2t，

设PQ＝a，则PE＝a，DE＝DP﹣a＝2﹣a，

∵△AEP∽△CED，

∴，

即，

解得，a＝，

∴PQ＝，

∴，

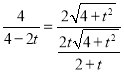解得，t1＝﹣﹣1（舍去），t2＝﹣1，

即t的值是﹣1．