题目内容
【题目】如图，上、下底面为全等的正六边形礼盒，其主视图与左视图均由矩形构成，主视图中大矩形边长如图所示，左视图中包含两个全等的矩形，如果用彩色胶带按如图所示的方式包扎礼盒，那么所需胶带长度至少为多少厘米？(结果精确到1 cm)
【答案】432cm
【解析】分析：由主视图知道，高是20 cm，两顶点之间的最大距离为60 cm，应利用正六边形的性质求得底面对边之间的距离，然后所有棱长相加即可.
本题解析：
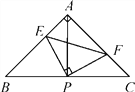
根据题意，作出实际图形的上底面，如解图．AC，CD是上底面的两边，过点C作CB⊥AD于点B.易得∠ACD＝120°，AC＝CD，CB⊥AD，∴∠CDB＝30°，∴CB＝
CD.
∵最长对角线长60 cm，∴2CB＋CD＝60 cm，∴CB＝15 cm，CD＝30 cm，∴BD＝15
，∴AD＝30 cm.∴胶带的长至少为30×6＋20×6≈432(cm)
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】有这样一个问题：探究函数y=-
+|x|的图象与性质．
小军根据学习函数的经验，对函数y=-+|x|的图象与性质进行了探究．
下面是小军的探究过程，请补充完整：
（1）函数y=-+|x|的自变量x的取值范围是 ；
（2）表是y与x的几组对应值.
x | -2 | -1.9 | -1.5 | -1 | -0.5 | 0 | 1 | 2 | 3 | 4 | … |
y | 2 | 1.60 | 0.80 | 0 | -0.72 | -1.41 | -0.37 | 0 | 0.76 | 1.55 | … |
在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
（3）观察图象，函数的最小值是 ；
（4）进一步探究，结合函数的图象，写出该函数的一条性质（函数最小值除外）： ．
