题目内容
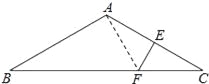
【题目】如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.

【答案】证明详见解析.
【解析】试题分析:利用辅助线,连接AF,求出CF=AF,∠BAF=90°,再根据AB=AC,∠BAC=120°可求出∠B的度数,由直角三角形的性质即可求出BF=2AF=2CF.
试题解析:连接AF,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=![]() =30°,
=30°,
∵AC的垂直平分线EF交AC于点E,交BC于点F,
∴CF=AF(线段垂直平分线上的点到线段两端点的距离相等),
∴∠FAC=∠C=30°(等边对等角),
∴∠BAF=∠BAC﹣∠FAC=120°﹣30°=90°,
在Rt△ABF中,∠B=30°,
∴BF=2AF(在直角三角形中,30°角所对的直角边等于斜边的一半),
∴BF=2CF(等量代换).

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目