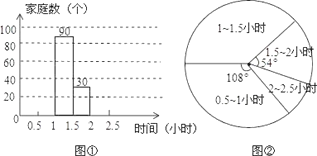
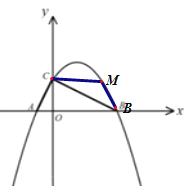
题目内容
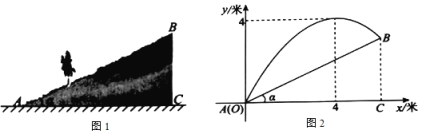
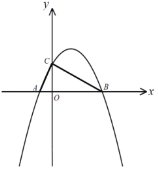
【题目】如图,已知抛物线![]() 与x轴交于点A、B,与y轴分别交于点C,其中点
与x轴交于点A、B,与y轴分别交于点C,其中点![]() ,点
,点![]() ,且
,且![]() .
.
(1)求抛物线的解析式;
(2)点P是线段AB上一动点,过P作![]() 交BC于D,当
交BC于D,当![]() 面积最大时,求点P的坐标;
面积最大时,求点P的坐标;
(3)点M是位于线段BC上方的抛物线上一点,当![]() 恰好等于
恰好等于![]() 中的某个角时,求点M的坐标.
中的某个角时,求点M的坐标.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,S最大,此时
时,S最大,此时![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)先根据射影定理求出点![]() ,设抛物线的解析式为:
,设抛物线的解析式为:![]() ,将点
,将点![]() 代入求出
代入求出![]() ,然后化为一般式即可;
,然后化为一般式即可;
(2)过点P作y轴的平行线交BC于点E,设![]() ,用待定系数法分别求出直线BC,直线AC,直线PD的解析式,表示出点E,点D的坐标,然后根据三角形面积公式列出二次函数解析式,利用二次函数的性质求解即可;
,用待定系数法分别求出直线BC,直线AC,直线PD的解析式,表示出点E,点D的坐标,然后根据三角形面积公式列出二次函数解析式,利用二次函数的性质求解即可;
(3)分两种情况求解:当![]() 时和当
时和当![]() 时.
时.
(1)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴由射影定理可得:![]() ,
,
∴![]() ,∴点
,∴点![]() ,
,
设抛物线的解析式为:![]() ,将点
,将点![]() 代入上式得:
代入上式得:![]() ,
,
∴抛物线的解析式为:![]() ;
;
(2)过点P作y轴的平行线交BC于点E,设![]() ,
,
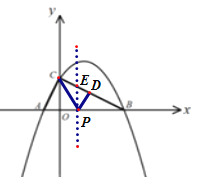
设![]() ,
,
把![]() ,
,![]() 代入得
代入得
![]() ,
,
∴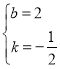 ,
,
∴![]() ,
,
∴![]() ,
,
同样的方法可求![]() ,
,
故可设![]() ,把
,把![]() 代入得
代入得![]() ,
,
联立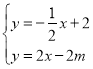 解得:
解得: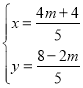 ,
,
∴![]() ,
,
![]() ,
,
故当![]() 时,S最大,此时
时,S最大,此时![]() ;
;
(3)由题知,![]() ,
,
当![]() 时,
时,![]() ,
,
∴点C与点M关于对称轴对称,
∴![]() ;
;
当![]() 时,过M作
时,过M作![]() 于F,过F作y轴的平行线,交x轴于G,交过M平行于x轴的直线于K,
于F,过F作y轴的平行线,交x轴于G,交过M平行于x轴的直线于K,
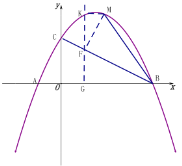
∵∠![]() ,BFM=∠BGF,
,BFM=∠BGF,
∴△MFK∽△FGB,
同理可证:![]() ,
,
∴![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,代入
,代入![]() ,
,
解得
![]() ,或
,或![]() (舍去),
(舍去),
∴![]() ,
,
故![]() 或
或![]() .
.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目