ΧβΡΩΡΎ»ί
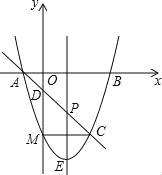
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§≈ΉΈοœΏy=ax2+bx+cΒΡΆΦœσ”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ®ΒψA‘ΎΒψBΒΡΉσ±ΏΘ©Θ§”κy÷αΫΜ”ΎΒψCΘ§ΒψAΓΔCΒΡΉχ±ξΖ÷±πΈΣΘ®-1Θ§0Θ©Θ§Θ®0Θ§-3Θ©Θ§÷±œΏx=1ΈΣ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΘ°ΒψDΈΣ≈ΉΈοœΏΒΡΕΞΒψΘ§÷±œΏBC”κΕ‘≥Τ÷αœύΫœ”ΎΒψEΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω Ϋ≤Δ÷±Ϋ”–¥≥ωΒψDΒΡΉχ±ξΘΜ
Θ®2Θ©ΒψPΈΣ÷±œΏx=1”“ΖΫ≈ΉΈοœΏ…œΒΡ“ΜΒψΘ®ΒψP≤Μ”κΒψB÷ΊΚœΘ©Θ°Φ«AΓΔBΓΔCΓΔPΥΡΒψΥυΙΙ≥…ΒΡΥΡ±Ώ–ΈΟφΜΐΈΣSΘ§»τS=![]() SΓςBCDΘ§«σΒψPΒΡΉχ±ξΘΜ
SΓςBCDΘ§«σΒψPΒΡΉχ±ξΘΜ
Θ®3Θ©ΒψQ «œΏΕΈBD…œΒΡΕ·ΒψΘ§ΫΪΓςDEQ―”±ΏEQΖ≠’έΒΟΒΫΓςDΓδEQΘ§ «Ζώ¥φ‘ΎΒψQ ΙΒΟΓςDΓδEQ”κΓςBEQΒΡ÷ΊΒΰ≤ΩΖ÷ΆΦ–ΈΈΣ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωBQΒΡ≥ΛΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩ(1)y=x2-2x-3Θ§ΕΞΒψDΒΡΉχ±ξΈΣΘ®1Θ§-4Θ©ΘΜΘ®2Θ©PΒψΉχ±ξΈΣΘ®![]() Θ§
Θ§![]() Θ©ΜρΘ®
Θ©ΜρΘ®![]() Θ§
Θ§![]() Θ©ΘΜΘ®3Θ©¥φ‘ΎΘ§
Θ©ΘΜΘ®3Θ©¥φ‘ΎΘ§![]() Μρ
Μρ![]() 1Μρ
1Μρ![]() -
-![]() Θ§
Θ§
ΓΨΫβΈωΓΩ
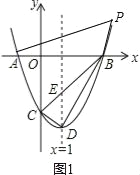
‘ΧβΖ÷ΈωΘΚΘ®1Θ©άϊ”Ο≈ΉΈοœΏΒΡΕ‘≥Τ–‘ΒΟΒΫBΘ®3Θ§0Θ©Θ§‘ρ…ηΫΜΒψ ΫΈΣy=aΘ®x+1Θ©Θ®x-3Θ©Θ§Α―CΘ®0Θ§-3Θ©¥ζ»κ«σ≥ωaΦ¥Ω…ΒΟΒΫ≈ΉΈοœΏΫβΈω ΫΘ§»ΜΚσΑ―ΫβΈω Ϋ≈δ≥…ΕΞΒψ ΫΦ¥Ω…ΒΟΒΫDΒψΉχ±ξΘΜ
Θ®2Θ©…ηPΘ®mΘ§m2-2m-3Θ©Θ§œ»»ΖΕ®÷±œΏBCΒΡΫβΈω Ϋy=x-3Θ§‘Ό»ΖΕ®EΘ®1Θ§-2Θ©Θ§‘ρΩ…ΗυΨί»ΐΫ«–ΈΟφΜΐΙΪ ΫΦΤΥψ≥ωSΓςBDC=SΓςBDE+SΓςCDE=3Θ§»ΜΚσΖ÷άύΧ÷¬έΘΚΒ±ΒψP‘Ύx÷α…œΖΫ ±Θ§Φ¥mΘΨ3Θ§»γΆΦ1Θ§άϊ”ΟS=SΓςPAB+SΓςCAB=![]() SΓςBCDΒΟΒΫ2m2-4m=
SΓςBCDΒΟΒΫ2m2-4m=![]() ΘΜΒ±ΒψP‘Ύx÷αœ¬ΖΫ ±Θ§Φ¥1ΘΦmΘΦ3Θ§»γΆΦ2Θ§Ν§ΫαOPΘ§άϊ”ΟS=SΓςAOC+SΓςCOP+SΓςPOB=
ΘΜΒ±ΒψP‘Ύx÷αœ¬ΖΫ ±Θ§Φ¥1ΘΦmΘΦ3Θ§»γΆΦ2Θ§Ν§ΫαOPΘ§άϊ”ΟS=SΓςAOC+SΓςCOP+SΓςPOB=![]() SΓςBCDΒΟΒΫ-
SΓςBCDΒΟΒΫ-![]() m2+
m2+![]() m+6=
m+6=![]() Θ§‘ΌΖ÷±πΫβΙΊ”ΎmΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χ«σ≥ωmΘ§¥”ΕχΒΟΒΫPΒψΉχ±ξΘΜ
Θ§‘ΌΖ÷±πΫβΙΊ”ΎmΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χ«σ≥ωmΘ§¥”ΕχΒΟΒΫPΒψΉχ±ξΘΜ
Θ®3Θ©¥φ‘ΎΘ°÷±œΏx=1ΫΜx÷α”ΎFΘ§άϊ”ΟΝΫΒψΦδΒΡΨύάκΙΪ ΫΦΤΥψ≥ωBD=2![]() Θ§Ζ÷άύΧ÷¬έΘΚΔΌ»γΆΦ3Θ§EQΓΆDB”ΎQΘ§÷ΛΟςRtΓςDEQΓΉRtΓςDBFΘ§άϊ”ΟœύΥΤ±»Ω…ΦΤΥψ≥ωDQ=
Θ§Ζ÷άύΧ÷¬έΘΚΔΌ»γΆΦ3Θ§EQΓΆDB”ΎQΘ§÷ΛΟςRtΓςDEQΓΉRtΓςDBFΘ§άϊ”ΟœύΥΤ±»Ω…ΦΤΥψ≥ωDQ=![]() Θ§‘ρBQ=BD-DQ=
Θ§‘ρBQ=BD-DQ=![]() ΘΜΔΎ»γΆΦ4Θ§EDΓδΓΆBD”ΎHΘ§÷ΛΟςRtΓςDEQ=HΓΉRtΓςDBFΘ§άϊ”ΟœύΥΤ±»ΦΤΥψ≥ωDH=
ΘΜΔΎ»γΆΦ4Θ§EDΓδΓΆBD”ΎHΘ§÷ΛΟςRtΓςDEQ=HΓΉRtΓςDBFΘ§άϊ”ΟœύΥΤ±»ΦΤΥψ≥ωDH=![]() Θ§EH=
Θ§EH=![]() Θ§‘ΎRtΓςQHDΓδ÷–Θ§…ηQH=xΘ§DΓδQ=DQ=DH-HQ=
Θ§‘ΎRtΓςQHDΓδ÷–Θ§…ηQH=xΘ§DΓδQ=DQ=DH-HQ=![]() -xΘ§DΓδH=DΓδE-EH=DE-EH=2-
-xΘ§DΓδH=DΓδE-EH=DE-EH=2-![]() Θ§‘ράϊ”ΟΙ¥Ι…Ε®άμΩ…ΒΟx2+Θ®2-
Θ§‘ράϊ”ΟΙ¥Ι…Ε®άμΩ…ΒΟx2+Θ®2-![]() Θ©2=Θ®
Θ©2=Θ®![]() -xΘ©2Θ§ΫβΒΟx=1-
-xΘ©2Θ§ΫβΒΟx=1-![]() Θ§”Ύ «BQ=BD-DH+HQ-
Θ§”Ύ «BQ=BD-DH+HQ-![]() =
=![]() +1ΘΜΔέ»γΆΦ5Θ§DΓδQΓΆBC”ΎGΘ§ΉςEIΓΆBD”ΎIΘ§άϊ”ΟΔΌΒΟΫα¬έΩ…ΒΟEI=
+1ΘΜΔέ»γΆΦ5Θ§DΓδQΓΆBC”ΎGΘ§ΉςEIΓΆBD”ΎIΘ§άϊ”ΟΔΌΒΟΫα¬έΩ…ΒΟEI=![]() Θ§BI=
Θ§BI=![]() Θ§ΕχBE=2
Θ§ΕχBE=2![]() Θ§‘ρBG=BE-EG=2
Θ§‘ρBG=BE-EG=2![]() -
-![]() Θ§ΗυΨί’έΒΰ–‘÷ ΒΟΓœEQD=ΓœEQDΓδΘ§‘ρΗυΨίΫ«ΤΫΖ÷œΏ–‘÷ ΒΟEG=EI=
Θ§ΗυΨί’έΒΰ–‘÷ ΒΟΓœEQD=ΓœEQDΓδΘ§‘ρΗυΨίΫ«ΤΫΖ÷œΏ–‘÷ ΒΟEG=EI=![]() Θ§Ϋ”Ή≈÷ΛΟςΓςBQGΓΉΓςBEIΘ§άϊ”ΟœύΥΤ±»Ω…ΒΟBQ=
Θ§Ϋ”Ή≈÷ΛΟςΓςBQGΓΉΓςBEIΘ§άϊ”ΟœύΥΤ±»Ω…ΒΟBQ=![]() -
-![]() Θ§Υυ“‘Β±BQΈΣ
Θ§Υυ“‘Β±BQΈΣ![]() Μρ
Μρ![]() +1Μρ
+1Μρ![]() -
-![]() ±Θ§ΫΪΓςDEQ―Ί±ΏEQΖ≠’έΒΟΒΫΓςDΓδEQΘ§ ΙΒΟΓςDΓδEQ”κΓςBEQΒΡ÷ΊΒΰ≤ΩΖ÷ΆΦ–ΈΈΣ÷±Ϋ«»ΐΫ«–ΈΘ°
±Θ§ΫΪΓςDEQ―Ί±ΏEQΖ≠’έΒΟΒΫΓςDΓδEQΘ§ ΙΒΟΓςDΓδEQ”κΓςBEQΒΡ÷ΊΒΰ≤ΩΖ÷ΆΦ–ΈΈΣ÷±Ϋ«»ΐΫ«–ΈΘ°
‘ΧβΫβΈωΘΚΘ®1Θ©ΓΏΒψA”κΒψBΙΊ”Ύ÷±œΏx=1Ε‘≥ΤΘ§
ΓύBΘ®3Θ§0Θ©Θ§
…η≈ΉΈοœΏΫβΈω ΫΈΣy=aΘ®x+1Θ©Θ®x-3Θ©Θ§
Α―CΘ®0Θ§-3Θ©¥ζ»κΒΟ-3a=-3Θ§ΫβΒΟa=1Θ§
Γύ≈ΉΈοœΏΨΆ–ΠΉ≈ΥΒΈΣy=Θ®x+1Θ©Θ®x-3Θ©=x2-2x-3Θ§
ΓΏy=Θ®x-1Θ©2-4Θ§
Γύ≈ΉΈοœΏΕΞΒψDΒΡΉχ±ξΈΣΘ®1Θ§-4Θ©ΘΜ
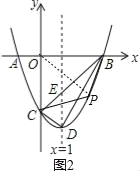
Θ®2Θ©…ηPΘ®mΘ§m2-2m-3Θ©Θ§“ΉΒΟ÷±œΏBCΒΡΫβΈω ΫΈΣy=x-3Θ§
Β±x=1 ±Θ§y=x-3=-3Θ§‘ρEΘ®1Θ§-2Θ©Θ§
ΓύSΓςBDC=SΓςBDE+SΓςCDE=![]() ΓΝ3ΓΝΘ®-2+4Θ©=3Θ§
ΓΝ3ΓΝΘ®-2+4Θ©=3Θ§
Β±ΒψP‘Ύx÷α…œΖΫ ±Θ§Φ¥mΘΨ3Θ§»γΆΦ1Θ§
S=SΓςPAB+SΓςCAB=![]() 3Θ®3+1Θ©+
3Ȯ3+1ȩ+![]() Ȯ3+1ȩȮm2-2m-3ȩ=2m2-4mȧ
Ȯ3+1ȩȮm2-2m-3ȩ=2m2-4mȧ
ΓΏS=![]() SΓςBCDΘ§
SΓςBCDΘ§
Γύ2m2-4m=![]() Θ§
Θ§
’ϊάμΒΟ4m2-8m-15=0Θ§ΫβΒΟm1=![]() Θ§m2=
Θ§m2=![]() Θ®…α»ΞΘ©Θ§
Θ®…α»ΞΘ©Θ§
ΓύPΒψΉχ±ξΈΣΘ®![]() Θ§
Θ§![]() Θ©ΘΜ
Θ©ΘΜ
Β±ΒψP‘Ύx÷αœ¬ΖΫ ±Θ§Φ¥1ΘΦmΘΦ3Θ§»γΆΦ2Θ§Ν§ΫαOPΘ§
S=SΓςAOC+SΓςCOP+SΓςPOB=![]() 31+
31+![]() 3m+
3m+![]() 3Θ®-m2+2m+3Θ©=-
3Θ®-m2+2m+3Θ©=-![]() m2+
m2+![]() m+6Θ§
m+6Θ§
ΓΏS=![]() SΓςBCDΘ§
SΓςBCDΘ§
Γύ-![]() m2+
m2+![]() m+6=
m+6=![]() Θ§
Θ§
’ϊάμΒΟm2-3m+1=0Θ§ΫβΒΟm1=![]() Θ§m2=
Θ§m2=![]() Θ®…α»ΞΘ©
Θ®…α»ΞΘ©
ΓύPΒψΉχ±ξΈΣΘ®![]() Θ§
Θ§![]() Θ©Θ§
Θ©Θ§
Ήέ…œΥυ ωΘ§PΒψΉχ±ξΈΣΘ®![]() Θ§
Θ§![]() Θ©ΜρΘ®
Θ©ΜρΘ®![]() Θ§
Θ§![]() Θ©ΘΜ
Θ©ΘΜ
Θ®3Θ©¥φ‘ΎΘ°÷±œΏx=1ΫΜx÷α”ΎFΘ§BD=![]() Θ§
Θ§
ΔΌ»γΆΦ3Θ§EQΓΆDB”ΎQΘ§ΓςDEQ―Ί±ΏEQΖ≠’έΒΟΒΫΓςDΓδEQΘ§

ΓΏΓœEDQ=ΓœBDFΘ§
ΓύRtΓςDEQΓΉRtΓςDBFΘ§
Γύ![]() Θ§Φ¥
Θ§Φ¥![]() Θ§ΫβΒΟDQ=
Θ§ΫβΒΟDQ=![]() Θ§
Θ§
ΓύBQ=BD-DQ=2![]() -
-![]() =
=![]() ΘΜ
ΘΜ
ΔΎ»γΆΦ4Θ§EDΓδΓΆBD”ΎHΘ§
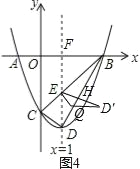
ΓΏΓœEDH=ΓœBDFΘ§
ΓύRtΓςDEQ=HΓΉRtΓςDBFΘ§
Γύ![]() Θ§Φ¥
Θ§Φ¥![]() Θ§ΫβΒΟDH=
Θ§ΫβΒΟDH=![]() Θ§EH=
Θ§EH=![]() Θ§
Θ§
‘ΎRtΓςQHDΓδ÷–Θ§…ηQH=xΘ§DΓδQ=DQ=DH-HQ=![]() -xΘ§DΓδH=DΓδE-EH=DE-EH=2-
-xΘ§DΓδH=DΓδE-EH=DE-EH=2-![]() Θ§
Θ§
Γύx2+Θ®2-![]() Θ©2=Θ®
Θ©2=Θ®![]() -xΘ©2Θ§ΫβΒΟx=1-
-xΘ©2Θ§ΫβΒΟx=1-![]() Θ§
Θ§
ΓύBQ=BD-DQ=BD-Θ®DH-HQΘ©=BD-DH+HQ=2![]() -
-![]() +1-
+1-![]() =
=![]() +1ΘΜ
+1ΘΜ
Δέ»γΆΦ5Θ§DΓδQΓΆBC”ΎGΘ§ΉςEIΓΆBD”ΎIΘ§”…ΔΌΒΟEI=![]() Θ§BI=
Θ§BI=![]() Θ§
Θ§
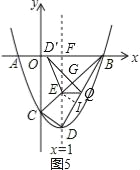
ΓΏBE=![]() Θ§
Θ§
ΓύBG=BE-EG=2![]() -
-![]() Θ§
Θ§
ΓΏΓςDEQ―Ί±ΏEQΖ≠’έΒΟΒΫΓςDΓδEQΘ§
ΓύΓœEQD=ΓœEQDΓδΘ§
ΓύEG=EI=![]() Θ§
Θ§
ΓΏΓœGBQ=ΓœIBEΘ§
ΓύΓςBQGΓΉΓςBEIΘ§
Γύ![]() Θ§Φ¥
Θ§Φ¥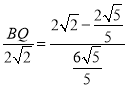
ΓύBQ=![]() -
-![]() Θ§
Θ§
Ήέ…œΥυ ωΘ§Β±BQΈΣ![]() Μρ
Μρ![]() 1Μρ
1Μρ![]() -
-![]() Θ§ΫΪΓςDEQ―Ί±ΏEQΖ≠’έΒΟΒΫΓςDΓδEQΘ§ ΙΒΟΓςDΓδEQ”κΓςBEQΒΡ÷ΊΒΰ≤ΩΖ÷ΆΦ–ΈΈΣ÷±Ϋ«»ΐΫ«–ΈΘ°
Θ§ΫΪΓςDEQ―Ί±ΏEQΖ≠’έΒΟΒΫΓςDΓδEQΘ§ ΙΒΟΓςDΓδEQ”κΓςBEQΒΡ÷ΊΒΰ≤ΩΖ÷ΆΦ–ΈΈΣ÷±Ϋ«»ΐΫ«–ΈΘ°

 Ής“ΒΗ®ΒΦœΒΝ–¥πΑΗ
Ής“ΒΗ®ΒΦœΒΝ–¥πΑΗ Ά§≤Ϋ―ßΒδ“ΜΩΈΕύΝΖœΒΝ–¥πΑΗ
Ά§≤Ϋ―ßΒδ“ΜΩΈΕύΝΖœΒΝ–¥πΑΗ