题目内容
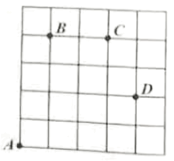
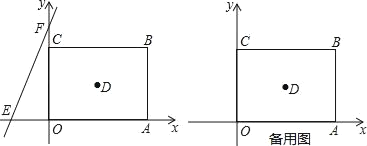
【题目】如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a、b、c分别满足﹣(a﹣4)2≥0,c=![]() +8.
+8.
(1)求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标;
(2)直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
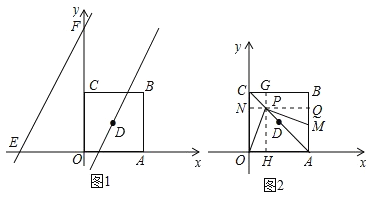
(3)点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,求![]() 的值.
的值.
【答案】(1)y=2x+8,D(2,2);(2)存在,5;(3)![]() .
.
【解析】
试题(1)利用非负数的性质求出a,b,c的值,进而确定出直线y=bx+c,得到正方形的边长,即可确定出D坐标;
(2)存在,理由为:对于直线y=2x+8,令y=0求出x的值,确定出E坐标,根据题意得:当直线EF平移到过D点时正好平分正方形AOBC的面积,设平移后的直线方程为y=2x+t,将D坐标代入求出b的值,确定出平移后直线解析式,进而确定出此直线与x轴的交点,从而求出平移距离,得到t的值;
过P点作PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,利用同角的余角相等得到一对角相等,再由一对直角相等,利用角平分线定理得到PH=PQ,利用AAS得到三角形OPH与三角形MPQ全等,得到OH=QM,根据四边形CNPG为正方形,得到PG=BQ=CN,由三角形CGP为等腰直角三角形得到CP=![]() GP=
GP=![]() BM,即可求出所求式子的值.
BM,即可求出所求式子的值.
试题解析:(1)∵-(a-4)2≥0,![]() ,
,
∴a=4,b=2,c=8,
∴直线y=bx+c的解析式为:y=2x+8,
∵正方形OABC的对角线的交点D,且正方形边长为4,
∴D(2,2);
(2)存在,理由为:
对于直线y=2x+8,
当y=0时,x=-4,
∴E点的坐标为(-4,0),
根据题意得:当直线EF平移到过D点时正好平分正方形AOBC的面积,
设平移后的直线为y=2x+t,
代入D点坐标(2,2),
得:2=4+t,即t=-2,
∴平移后的直线方程为y=2x-2,
令y=0,得到x=1,
∴此时直线和x轴的交点坐标为(1,0),平移的距离为1-(-4)=5,
则t=5秒;
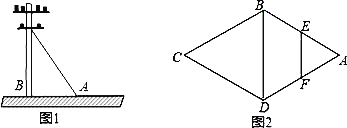
(3)过P点作PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,
∵∠OPM=∠HPQ=90°,
∴∠OPH+∠HPM=90°,∠HPM+∠MPQ=90°,
∴∠OPH=∠MPQ,
∵AC为∠BAO平分线,且PH⊥OA,PQ⊥AB,
∴PH=PQ,
在△OPH和△MPQ中,
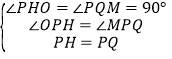 ,
,
∴△OPH≌△MPQ(AAS),
∴OH=QM,
∵四边形CNPG为正方形,
∴PG=BQ=CN,
∴CP=![]() PG=
PG=![]() BM,
BM,
即![]() .
.

【题目】一辆出租车从甲地出发,在一条东西走向的街道上往返行驶,每次行驶的路程(记向东为正),记录如下表(![]() ,单位:
,单位:![]() ):
):
第1次 | 第2次 | 第3次 | 第4次 |
|
|
|
|
(1)说出这辆出租车每次行驶的方向.
(2)这辆出租车共行驶了多少路程?
【题目】事业单位人员编制连进必考,现一事业单位需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方而进行量化考核.甲、乙、丙各项得分如下表:
笔试 | 面试 | 体能 | |
甲 | 84 | 80 | 88 |
乙 | 94 | 92 | 69 |
丙 | 81 | 84 | 78 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序;
(2)该单位规定:笔试、面试、体能分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分.根据规定,请你说明谁将被录用.