��Ŀ����
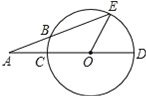
����Ŀ����ͼ����ֱ֪��l��y=��![]() x+b��x�ᡢy��ֱ��ڵ�A��B��ֱ��l1��y=
x+b��x�ᡢy��ֱ��ڵ�A��B��ֱ��l1��y=![]() x+1��y�ύ�ڵ�C����ֱ��l��ֱ��l1�Ľ���ΪE
x+1��y�ύ�ڵ�C����ֱ��l��ֱ��l1�Ľ���ΪE
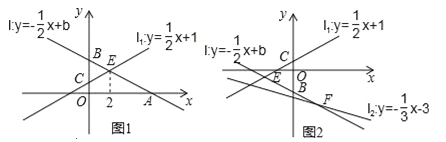
��1����ͼ1������E�ĺ�����Ϊ2�����A�����ꣻ
��2���ڣ�1����ǰ���£�D��a��0��Ϊx���ϵ�һ�㣬����D��x��Ĵ��ߣ��ֱ�ֱ��l��ֱ��l1�ڵ�M��N�����Ե�B��C��M��NΪ������ı���Ϊƽ���ı��Σ���a��ֵ��
��3����ͼ2����ֱ��l��ֱ��l2��y=��![]() x��3�Ľ���ΪF�����Ƿ���ڵ�B��ʹBE=BF�������ڣ����ֱ��l�Ľ���ʽ���������ڣ���˵�����ɣ�
x��3�Ľ���ΪF�����Ƿ���ڵ�B��ʹBE=BF�������ڣ����ֱ��l�Ľ���ʽ���������ڣ���˵�����ɣ�
���𰸡���1����A������Ϊ��6��0����
��2�����Ե�B��C��M��NΪ������ı���Ϊƽ���ı��Σ�a��ֵΪ4��
��3�����ڵ�B��ʹBE=BF����ʱֱ��l�Ľ���ʽΪy=��![]() x��
x��![]() ��
��
�������������������1���ɵ�E�ĺ�������һ�κ���ͼ���ϵ���������������ҳ���E�����꣬�����ô���ϵ�����������ֱ��![]() �Ľ���ʽ����
�Ľ���ʽ����![]() ���
���![]() ��ֵ�����ɵó���A�����ꣻ
��ֵ�����ɵó���A�����ꣻ
��2�����ݵ�D�ĺ�����Ϊa����һ�κ���ͼ���ϵ���������������ҳ���M��N�����꣬�Ӷ��ó��߶�MN�ij��ȣ��ֱ���ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��![]() �����
�����![]() �����꣬�ٸ���ƽ���ı��ε����ʼ��ɵó�����a�ĺ�����ֵ���ŵ�һԪһ�η��̣��ⷽ�̼��ɵó����ۣ�
�����꣬�ٸ���ƽ���ı��ε����ʼ��ɵó�����a�ĺ�����ֵ���ŵ�һԪһ�η��̣��ⷽ�̼��ɵó����ۣ�
��3��������ڣ�����ֱ��![]() �Ľ���ʽ�ɷ����飬�ⷽ���������E�����꣬����ֱ��
�Ľ���ʽ�ɷ����飬�ⷽ���������E�����꣬����ֱ��![]() �Ľ���ʽ�ɷ����飬�ⷽ���������F�����꣬���
�Ľ���ʽ�ɷ����飬�ⷽ���������F�����꣬���![]() ���ɵó�����b��һԪһ�η��̣��ⷽ�����bֵ������ý⣮
���ɵó�����b��һԪһ�η��̣��ⷽ�����bֵ������ý⣮
���������(1)�ߵ�E��ֱ��l1�ϣ��ҵ�E�ĺ�����Ϊ2��
���E������Ϊ(2,2)��
�ߵ�E��ֱ��l�ϣ�
![]() ��ã�b=3��
��ã�b=3��
��ֱ��l�Ľ���ʽΪ![]()
��y=0ʱ,��![]()
��ã�x=6,
���A������Ϊ(6,0).
(2)�������⻭��ͼ�Σ���ͼ3��ʾ,
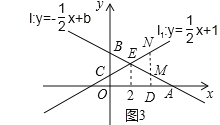
��x=aʱ��![]()
![]()
��x=0ʱ,![]()
��BC=31=2.
��BC��MN��
�൱MN=BC=2ʱ���Ե�B. C.M��NΪ������ı���Ϊƽ���ı��Σ�
��ʱ|a2|=2��
��ã�a=4��a=0(��ȥ).
�൱�Ե�B. C.M��NΪ������ı���Ϊƽ���ı��Σ�a��ֵΪ4.
(3)�������.
����ֱ��l��l1�Ľ���ʽ�ɷ�����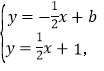
��ã�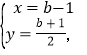
���E������Ϊ![]()
����ֱ��l��l2�Ľ���ʽ�ɷ���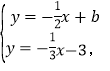
��ã�![]()
���F������Ϊ(18+6b,92b).
��BE=BF����E.F����ֱ��l�ϣ�
��b1=186b,��ã�![]()
��ʱֱ��l�Ľ���ʽΪ![]()
�ʴ��ڵ�B,ʹBE=BF,��ʱֱ��l�Ľ���ʽΪ![]()

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�