题目内容
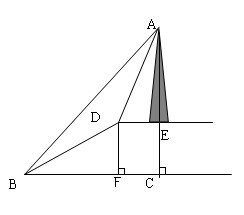
如图,小山的顶部是平地,在这块平地上有一高压输电线架,小山的斜坡BD的坡度i=1﹕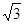 ,长度为50米。在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°。
,长度为50米。在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°。
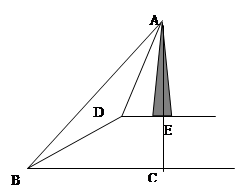
求: ①小山的高度CE。(4分)
②铁架的高度AE。(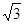 ≈1.73,精确到0.1米)。(5分)
≈1.73,精确到0.1米)。(5分)
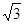 ,长度为50米。在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°。
,长度为50米。在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°。
求: ①小山的高度CE。(4分)
②铁架的高度AE。(
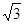 ≈1.73,精确到0.1米)。(5分)
≈1.73,精确到0.1米)。(5分)(1)、25(2)、43.3米
试题分析:(1)过点D做DF⊥BC,垂足为F。
依题意知坡度i=1﹕
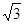 ,所以tanDBF=
,所以tanDBF=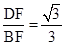 ,所以
,所以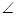 DBF=30°。所以Rt△DBF中,DF=
DBF=30°。所以Rt△DBF中,DF=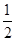 BD=25m,易知DE与BC为水平线,所以四边形DEFC为长方形,CE=DF=25m。
BD=25m,易知DE与BC为水平线,所以四边形DEFC为长方形,CE=DF=25m。(2)如图所示,
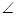 BDA=360°-
BDA=360°-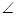 BDF-
BDF-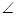 FDE-
FDE-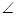 ADE=150°。又∵
ADE=150°。又∵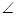 ABC=45°,
ABC=45°,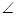 DBF=30°∴
DBF=30°∴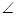 ABD=15°,∴
ABD=15°,∴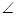 BAD=180°-
BAD=180°-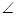 ABD-
ABD-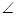 BDA=15°∴
BDA=15°∴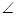 BAD=
BAD=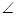 ABD,△ADB为等腰三角形,所以AD=BD=50m。在Rt△ADE中,∵
ABD,△ADB为等腰三角形,所以AD=BD=50m。在Rt△ADE中,∵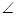 ADE=60°,∴AE=
ADE=60°,∴AE= =
= ≈43.3m
≈43.3m点评:难度中等,主要考查学生对直角三角形及三角函数的学习。分析题意,题(1)所求边长需要灵活转化为具有已知边长及特殊角度的直角三角形中的一条边。利用三角函数求出答案。题(2)中所求边长需要在该直角三角形至少有2个已知条件才能计算,说明要技巧性地先求出另外的斜边或者是直角边,通过已知条件,与已知条件关系较多的为斜边。所以求斜边是突破点。

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 .
.




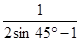 -2
-2 +sin260°+cos260°.
+sin260°+cos260°. 中,
中, ,
,
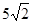 ,点
,点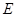 在
在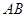 上,
上,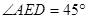 ,
,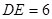 ,
,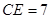 .求:
.求: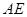 的长及
的长及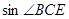 的值.
的值.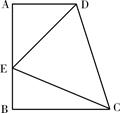
 的位置如图所示,则cosB的值为( )
的位置如图所示,则cosB的值为( )




 ,铁环钩与铁环相切点为
,铁环钩与铁环相切点为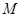 ,铁环与地面接触点为
,铁环与地面接触点为 ,
, ,且
,且 .
.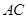 的高度
的高度 (单位:厘米);
(单位:厘米);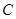 与点
与点 个单位,求铁环钩MP的长度(厘米).
个单位,求铁环钩MP的长度(厘米).