Question

【题目】如图，在平面直角坐标系中，已知 A（-2,0），B（0，m）两点，且线段AB= 2 ，以 AB 为边在第二象限内作正方形 ABCD。

（1）求点 B 的坐标

（2）在 x 轴上是否存在点 Q，使△QAB 是以 AB 为腰的等腰三角形？若存在，请直接写出点 Q 的坐标，若不存在，请说明理由；

（3）如果在坐标平面内有一点 P（a，3），使得△ABP 的面积与正方形 ABCD 的面 积相等，求 a 的值。

Answer 1

【答案】(1)（0，4）(2)存在，Q点坐标为（，0）或（，0）或（2，0）

(3) 或

【解析】

（1）因为三角形ABO为直角三角形，所以可依据勾股定理求出OB的长度，即可求出点B的坐标.

（2）当AB=AQ时，三角形QAB为等腰三角形，当BQ=AB时，三角形QAB为等腰三角形，再根据AB的长度分别求出点Q的坐标即可.

（3）由P（a，3）可知，p点在y=3直线上运动，画出简图，当a＞0和当a＜0时，分两种情况进行分析.

(1)由题意知AB=，AO=2，根据勾股定理得

,所以点B的坐标为（0，4）

（2）设Q点坐标为（m，0）

当AB=AQ时，即AQ==，解得：m=或

则此时Q点坐标为（，0）（，0）

当BQ=AB时，BQ=，解得：m=2或-2

而m=-2时与A点重合，则m=2.

则Q的坐标为（2，0）

（3）①

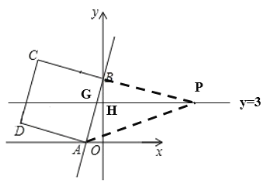
由题意可知p点坐标为（a，3），则p点再y=3这条直线上，连接BP，AP，y=3与y轴的交点为H，与直线AB的交点为G，当a大于0时，如图所示：

此时三角形APB的面积可以由三角形PBG与三角形PGA的面积和求得.

设AB直线的函数解析式为y=kx+b，代入点A(-2，0)，B(0,4)得：

则G点的纵坐标与P点的纵坐标相等，则把y=3代入，得x=

则此时G点坐标为（，3），则PG=a-=

则三角形PBG与三角形PGA的面积和为：GP×BH×+ GP×OH×= GP(BH+OH)= GP×BO=

即

解得：.

②

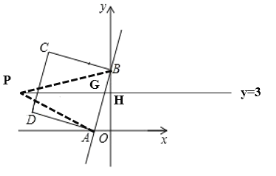
当a小于0时，如图所示：

同理①得：PG=-a

则此时有：GP(BH+OH)= GP×BO=

解得：

则综上所述：或