题目内容
【题目】如图,抛物线y=ax2+bx+c的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,-3),顶点为D.
(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和对称轴.
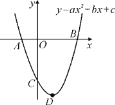
【答案】 (1) y=x-2x-3;(2) D (1,-4),对称轴是直线x=1.
【解析】
(1)根据抛物线与x轴的两个交点坐标可设二次函数交点式: y=a(x+1)(x-3),
然后根据抛物线又经过点点C(0,-3),将点C代入解析式可求出a,从而求出函数解析式,
(2)根据二次函数顶点坐标公式可直接求二次函数顶点和对称轴方程.
解:(1)设此抛物线的解析式是y=a(x+1)(x-3),
把点C(0,-3)代入,得
-3=a·1·(-3),
解得a=1,
∴y=(x+1)(x-3)=x2-2x-3.
(2)顶点D的坐标是(1,-4),对称轴是直线x=1.

练习册系列答案
相关题目