题目内容
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和格点P.
(1)以A点为位似中心,将△ABC在网格中放大成△AB1C1,使![]() =2,请画出△AB1C1;
=2,请画出△AB1C1;
(2)以P点为三角形的一个顶点,请画一个格点△PMN,使△PMN∽△ABC,且相似比为![]() .
.
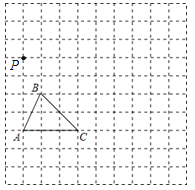
【答案】(1)答案见解析;(2)答案见解析.
【解析】【试题分析】(1)以A为位似中心,欲使![]() =2,即
=2,即![]() ,则△ABC与△AB1C1的相似比为
,则△ABC与△AB1C1的相似比为![]() ,即延长AB到B1 ,使AB=BB1,同样的方法,使AC=CC1,因为
,即延长AB到B1 ,使AB=BB1,同样的方法,使AC=CC1,因为![]() ,则△ABC
,则△ABC![]() △AB1C1,
△AB1C1,
(2)分别将个边长同时乘以![]() ,分别为
,分别为![]() ,利用勾股定理,分别找出来即可.
,利用勾股定理,分别找出来即可.
【试题解析】
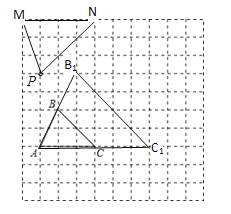
(1)如图,△AB1C1即为所求
(2)如图,△PMN即为所求(注意PM、PN、MN的长)。

【题目】有这样一个问题:探究函数![]() 的图象与性质.小华根据学习函数的经验,对函数
的图象与性质.小华根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
(2)下表是y与x的几组对应值.m的值为_______;
x | -2 |
| -1 |
|
|
| 1 | 2 | 3 | 4 | … |
y | 0 |
| m |
|
|
|
| 1 |
|
| … |
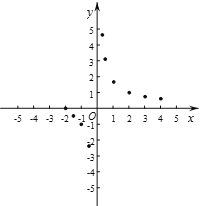
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的一条性质:____________.
(5)结合函数图象估计![]() 的解的个数为_______个.
的解的个数为_______个.
【题目】为了更好治理某湖水质,保护环境,市治污公司决定购买![]() 台污水处理设备.现有
台污水处理设备.现有![]() ,
,![]() 两种型号的设备,其中每台的价格,月处理污水量如下表.经调查:购买一台
两种型号的设备,其中每台的价格,月处理污水量如下表.经调查:购买一台![]() 型设备比购买一台
型设备比购买一台![]() 型设备多
型设备多![]() 万元,购买
万元,购买![]() 台
台![]() 型设备比购买
型设备比购买![]() 台
台![]() 型设备少
型设备少![]() 万元.
万元.
|
| |
价格(万元/台) |
|
|
处理污水量(吨/月) |
|
|
(![]() )求
)求![]() ,
,![]() 的值.
的值.
(![]() )经预算:市治污公司购买污水处理设备的资金不超过
)经预算:市治污公司购买污水处理设备的资金不超过![]() 万元,你认为该公司有哪几种购买方案.
万元,你认为该公司有哪几种购买方案.
(![]() )在(
)在(![]() )问的条件下,若每月要求处理该湖的污水量不低于
)问的条件下,若每月要求处理该湖的污水量不低于![]() 吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.