题目内容
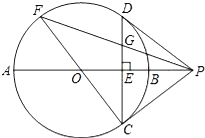
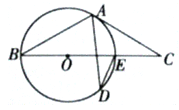
【题目】如图，BE是⊙O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点C
（I）若∠ADE=25°，求∠C的度数
（II）若AB=AC，求∠D的度数.
【答案】（1）40°（2）30°
【解析】
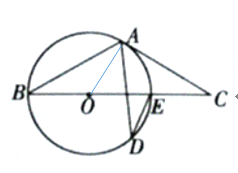
（1）连接OA，根据切线的性质知OA⊥AC，在根据圆周角定理知∠AOE=2∠ADE=50°，再利用直角三角形的锐角互余即可求出；（2）根据等腰三角形与圆周角定理即可求出.
（1）连接OA，
∵AC是⊙O的切线，OA是⊙O的半径，
∴OA⊥AC，
∵
，∠ADE=25°
∴∠AOE=2∠ADE=50°，
∴∠C=90°-∠AOE=40°.
（2）∵AB=AC，
∴∠B=∠C，
∵
∴∠AOC=2∠B，
∴∠AOC=2∠C，
∵∠OAC=90°，
∴∠AOC+∠C=90°，
∴3∠C=90°，
∴∠C=30°，
∴∠B=30°，
∴∠D=30°.
练习册系列答案
相关题目
