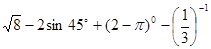题目内容
如图，⊙O的外切正六边形ABCDEF的边长为2，则图中阴影部分的面积为（ ）．
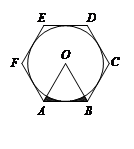
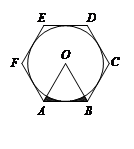
A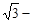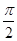．  | B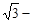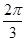． | C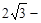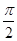． | D． |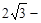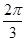
A
∵六边形ABCDEF是正六边形，
∴∠AOB=60°，
∴△OAB是等边三角形，OA=OB=AB=2，
设点G为AB与⊙O的切点，连接OG，则OG⊥AB，
∴OG=OA•sin60°=2×
= 
，
∴S阴影=S△OAB-S扇形OMN=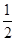
×2×-
．
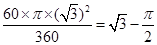故选A．
∴∠AOB=60°，
∴△OAB是等边三角形，OA=OB=AB=2，
设点G为AB与⊙O的切点，连接OG，则OG⊥AB，
∴OG=OA•sin60°=2×
= ，∴S阴影=S△OAB-S扇形OMN=
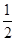×2×-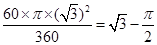．故选A．
练习册系列答案
习题精选系列答案
相关题目
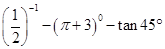
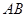，请用直尺和圆规作出线段
，
，
，
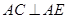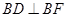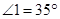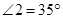.求证：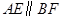
.
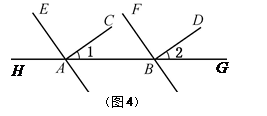
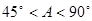，则下列各式成立的是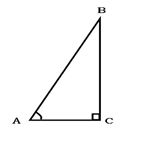
≈1.41，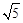
≈2.24)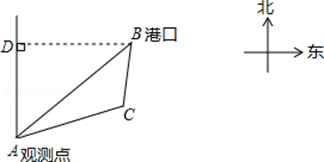
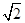≈1.414，
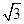≈1.732）
. 
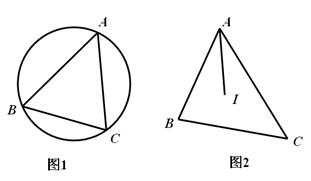
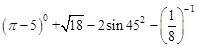