题目内容
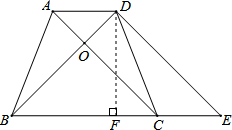
 (2013•深圳)如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,AC与BD交于点O,廷长BC到E,使得CE=AD,连接DE.
(2013•深圳)如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,AC与BD交于点O,廷长BC到E,使得CE=AD,连接DE.(1)求证:BD=DE.
(2)若AC⊥BD,AD=3,SABCD=16,求AB的长.
分析:(1)由AD∥BC,CE=AD,可得四边形ACED是平行四边形,即可证得AC=DE,又由等腰梯形的性质,可得AC=BD,即可证得结论;
(2)首先过点D作DF⊥BC于点F,可证得△BDE是等腰直角三角形,由SABCD=16,可求得BD的长,继而求得答案.
(2)首先过点D作DF⊥BC于点F,可证得△BDE是等腰直角三角形,由SABCD=16,可求得BD的长,继而求得答案.
解答:(1)证明:∵AD∥BC,CE=AD,
∴四边形ACED是平行四边形,
∴AC=DE,
∵四边形ABCD是等腰梯形,AD∥BC,AB=DC,
∴AC=BD,
∴BD=DE.
(2)解:过点D作DF⊥BC于点F,
∵四边形ACED是平行四边形,
∴CE=AD=3,AC∥DE,
∵AC⊥BD,
∴BD⊥DE,
∵BD=DE,
∴S△BDE=
BD•DE=
BD2=
BE•DF=
(BC+CE)•DF=
(BC+AD)•DF=S梯形ABCD=16,
∴BD=4
,
∴BE=
BD=8,
∴DF=BF=EF=
BE=4,
∴CF=EF-CE=1,
∴AB=CD=
=
.
∴四边形ACED是平行四边形,
∴AC=DE,
∵四边形ABCD是等腰梯形,AD∥BC,AB=DC,
∴AC=BD,
∴BD=DE.
(2)解:过点D作DF⊥BC于点F,

∵四边形ACED是平行四边形,
∴CE=AD=3,AC∥DE,
∵AC⊥BD,
∴BD⊥DE,
∵BD=DE,
∴S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴BD=4
| 2 |
∴BE=
| 2 |
∴DF=BF=EF=
| 1 |
| 2 |
∴CF=EF-CE=1,
∴AB=CD=
| CF2+DF2 |
| 17 |
点评:此题考查了等腰三角形的性质、等腰直角三角形的性质与判定、平行四边形的判定与性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 (2013•深圳)如图,有一张一个角为30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是( )
(2013•深圳)如图,有一张一个角为30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是( ) (2013•深圳)如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sinα的值是( )
(2013•深圳)如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sinα的值是( )