题目内容
 (2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是
(2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是| 11 |
| 3 |
| 11 |
| 3 |
分析:当射线AD与⊙C相切时,△ABE面积的最大.设EF=x,由切割线定理表示出DE,可证明△CDE∽△AOE,根据相似三角形的性质可求得x,然后求得△ABE面积.
解答:解:当射线AD与⊙C相切时,△ABE面积的最大.
连接AC,
∵∠AOC=∠ADC=90°,AC=AC,OC=CD,
∴Rt△AOC≌Rt△ADC(HL),
∴AD=AO=2,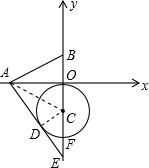
连接CD,设EF=x,
∴DE2=EF•OE,
∵CF=1,
∴DE=
,
∴△CDE∽△AOE,
∴
=
,
即
=
,
解得x=
,
S△ABE=
=
=
.
故答案为:
连接AC,
∵∠AOC=∠ADC=90°,AC=AC,OC=CD,
∴Rt△AOC≌Rt△ADC(HL),
∴AD=AO=2,

连接CD,设EF=x,
∴DE2=EF•OE,
∵CF=1,
∴DE=
| x(x+2) |
∴△CDE∽△AOE,
∴
| CD |
| AO |
| CE |
| AE |
即
| 1 |
| 2 |
| x+1 | ||
2+
|
解得x=
| 2 |
| 3 |
S△ABE=
| BE×AO |
| 2 |
2×(
| ||
| 2 |
| 11 |
| 3 |
故答案为:
| 11 |
| 3 |
点评:本题是一个动点问题,考查了切线的性质和三角形面积的计算,解题的关键是确定当射线AD与⊙C相切时,△ABE面积的最大.

练习册系列答案
相关题目