题目内容
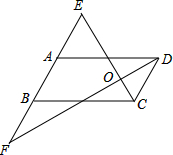 如图,在?ABCD中,AD=2AB,点E、A、B、F在同一条直线上,且EA=AB=BF,则CE⊥FD吗?说说你的理由.
如图,在?ABCD中,AD=2AB,点E、A、B、F在同一条直线上,且EA=AB=BF,则CE⊥FD吗?说说你的理由.考点:平行四边形的性质
专题:
分析:连接MN,根据EA=AB=BF,AD∥BC,可得AM为△EBC的中位线,BN为△FAD的中位线,可得AM=
BC=NC,BN=
AD=MD,然后根据AD=2AB,可得MD=AB=DC,可证明四边形MNCD为菱形,继而可得MC⊥ND,即CE⊥FD.
| 1 |
| 2 |
| 1 |
| 2 |
解答:答:CE⊥FD;
证明: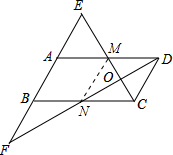 连接MN,
连接MN,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∵EA=AB=BF,
∴AM为△EBC的中位线,BN为△FAD的中位线,
即AM=
BC=NC,BN=
AD=MD,
∵AD=2AB,AD=BC,
∴MD=AB=DC,
∵AD∥BC,
∴四边形MNCD为菱形,
∴MC⊥ND,即CE⊥FD.
证明:
 连接MN,
连接MN,∵四边形ABCD为平行四边形,
∴AD∥BC,
∵EA=AB=BF,
∴AM为△EBC的中位线,BN为△FAD的中位线,
即AM=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD=2AB,AD=BC,
∴MD=AB=DC,
∵AD∥BC,
∴四边形MNCD为菱形,
∴MC⊥ND,即CE⊥FD.
点评:本题考查了平行四边形的性质以及菱形的判定,解答本题的关键是根据题目所给的条件,判定AM和BN为三角形的中位线,继而得出四边形MNCD为菱形.

练习册系列答案
相关题目
如果关于x的方程
+3=
有增根,则a的值是( )
| a |
| x-2 |
| 1-x |
| 2-x |
| A、2 | B、-2 | C、1 | D、±2 |
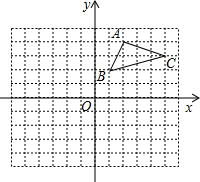 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题: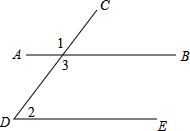 如图:已知∠1=120°,∠2=60°,那么图中哪两条直线平行?为什么?
如图:已知∠1=120°,∠2=60°,那么图中哪两条直线平行?为什么?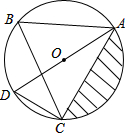 如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°,∠ACB=50°.请解答下列问题:
如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°,∠ACB=50°.请解答下列问题: