题目内容
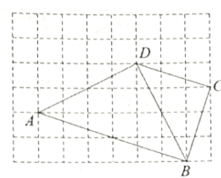
【题目】利用6×8正方形网格画图(不写画法,保留画图痕迹):
(1)画出![]() 的对称轴直线
的对称轴直线![]() ;
;
(2)画![]() ,使得
,使得![]() 与
与![]() 关于直线
关于直线![]() 对称;
对称;
(3)画格点![]() ,使得
,使得![]() 是以
是以![]() 为斜边的直角三角形。
为斜边的直角三角形。
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)先判断出△ABD为等腰直角三角形,再判断出格点M为AB中点,则过点D、M作直线即为对称轴l;
(2)先判断出CD⊥l,然后延长CD至E,使CD=DE,最后连接即可;
(3)根据∠AFB是直角且点F在格点上进行判断即可.
解:(1)由勾股定理得,![]() ,
,
∴△ABD为等腰直角三角形,
由勾股定理得,AM=![]() ,BM=
,BM=![]() ,AB=
,AB=![]() ,
,
∴AM=BM=![]() AB,即点M 为AB中点,
AB,即点M 为AB中点,
∴过点D、M作直线l即为△ABD的对称轴;
(2)∵△ABD为等腰直角三角形,直线l⊥AB,
∴直线l与BD相交所成锐角为45°,
∵由勾股定理得,![]() ,
,
∴△BCD为等腰直角三角形,则∠BDC=45°,
∴CD⊥l,
如图,延长CD至E,使CD=DE,连接AE,则△ADE即为所求;
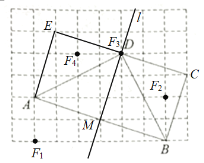
(3)如图,在△ABF1中,AF12=4,BF12=36,AB2=22+62=40,
∴AF12+BF12=AB2,
∴△ABF1是直角三角形,∠AF1B=90°,则点F1即为所求,
同理可得,点F2、F3、F4即为所求.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目


