��Ŀ����
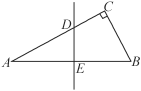
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y= ![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C�������ߵĶ���Ϊ��D������B��BC�Ĵ��ߣ����Գ����ڵ�E��
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C�������ߵĶ���Ϊ��D������B��BC�Ĵ��ߣ����Գ����ڵ�E��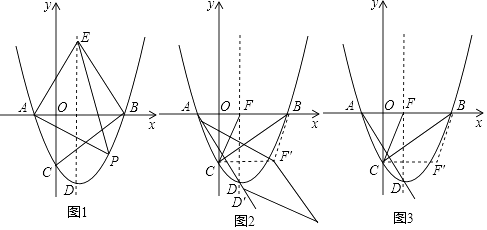
��1����֤����E���D����x��Գƣ�
��2����PΪ���������ڵ��������ϵ�һ���㣬����PAE��������ʱ���ڶԳ�������һ��M����y������һ��N��ʹ��OM+MN+NP��С�����ʱ��M�����꼰OM+MN+NP����Сֵ��
��3����ͼ2��ƽ�������ߣ�ʹ�����ߵĶ���D������AD���ƶ�����Dƽ�ƺ�Ķ�Ӧ��ΪD�䣬��A�Ķ�Ӧ��A�䣬�������ߵĶԳ�����x�ύ�ڵ�F������FBC��BC���ۣ�ʹ��F���ڵ�F�䴦����ƽ������һ��G������F�䡢G��D�䡢A��Ϊ������ı���Ϊ���Σ���ƽ�Ƶľ��룮
���𰸡�
��1��֤������ͼ1�У���y=0���õ� ![]() x2��
x2�� ![]() x��3=0�����x=��
x��3=0�����x=�� ![]() ��3
��3 ![]() ��
��

��A���� ![]() ��0����B��3
��0����B��3 ![]() ��0����
��0����
��x=0���ɵ�y=��3��
��C��0����3����
��y= ![]() x2��
x2�� ![]() x��3=
x��3= ![]() ��x��
��x�� ![]() ��2��4��
��2��4��
�ඥ��D�� ![]() ����4������Գ�����x�ύ��F����BF=2
����4������Գ�����x�ύ��F����BF=2 ![]() ��
��
�ߡ�EFB�ס�BOC��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��EF=4��
��E�� ![]() ��4����
��4����
��E��D����x��Գƣ�
��2������P��PQ��y�ᣬ��ֱ��AE�ڵ�Q��
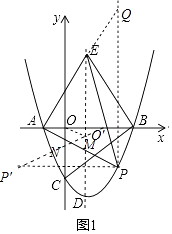
��yAE= ![]() x+2��
x+2��
����P��a�� ![]() a2��
a2�� ![]() a��3����Q��a��
a��3����Q��a�� ![]() a+2������0��a��3
a+2������0��a��3 ![]() ����
����
��PQ=�� ![]() a+2������
a+2������ ![]() a2��
a2�� ![]() a��3��=��
a��3��=�� ![]() a2+2
a2+2 ![]() a+5��
a+5��
��S��PAE= ![]() PQ|xE��xA|=
PQ|xE��xA|= ![]() ����
���� ![]() a2+2
a2+2 ![]() a+5��2
a+5��2 ![]() =��
=�� ![]() a2+4a+5
a2+4a+5 ![]() ��
��
�൱a=�� ![]() =2
=2 ![]() ʱ��S��PAE���ʱP��2
ʱ��S��PAE���ʱP��2 ![]() ����3����
����3����
����O���ڶԳ���ĶԳƵ�O�䣨2 ![]() ��0��������P����Y��ĶԳƵ�P�䣨��2
��0��������P����Y��ĶԳƵ�P�䣨��2 ![]() ����3��������O��P�䣬�ֱԳ��ᡢy���ڵ�M��N����ʱM��N��Ϊ����
����3��������O��P�䣬�ֱԳ��ᡢy���ڵ�M��N����ʱM��N��Ϊ����
��yP��O��= ![]() x��
x�� ![]() ����x=
����x= ![]() ʱ��y=��
ʱ��y=�� ![]() ��
��
��M�� ![]() ����
���� ![]() ����
����
��OM+MN+NP����СֵO��P��= ![]() =
= ![]() ��
��
��3����F�䣨 ![]() ����
���� ![]() ����A����
����A���� ![]() +
+ ![]() t����2t����D��
t����2t����D�� ![]() ����4����
����4����
��ƽ�ƾ���Ϊ ![]() t����A�䣨��
t����A�䣨�� ![]() +
+ ![]() t����2t����D�䣨
t����2t����D�䣨 ![]() +
+ ![]() t����4��2t����
t����4��2t����
A��F2=6t2��24t+ ![]() ��D��F��2=6t2+
��D��F��2=6t2+ ![]() ��A��D��2=24��
��A��D��2=24��
�ٵ�A��F2=D��F��2ʱ��6t2��24t+ ![]() =6t2+
=6t2+ ![]() �����t=1��
�����t=1��
�ڵ�A��F��2=A��D��2ʱ��6t2��24t+ ![]() =24�����t=
=24�����t= ![]() ��
��
�۵�D��F��2=A��D��2ʱ��24=6t2+ ![]() �����t=
�����t= ![]() ��
�� ![]() ����������
����������
��ƽ�Ƶľ��� ![]() t=
t= ![]() ��
�� ![]() ��
�� ![]() ��
��
����������1���������A��B��C��D�����꣬�ٸ��ݡ�EFB�ס�BOC��Ӧ�߳ɱ����ó����̣��Ƴ�EF�ij��ȣ������E�����꼴�ɽ�����⣻
��2������P��PQ��y�ᣬ��ֱ��AE�ڵ�Q������ ���κ��������ö��κ��������������P�����꣬����O���ڶԳ���ĶԳƵ�O�䣬����P����Y��ĶԳƵ�P�䣬����O��P�䣬�ֱԳ��ᡢy���ڵ�M��N����ʱM��N��Ϊ����
��3���������F,A,D��������꣬��ƽ�ƾ���Ϊ![]() t����ó�A�䣬D������꣬�ɵ�A��F2����D��F��2��A��D��2�ij��ȣ�Ȼ����������ٵ�A��F2=D��F��2ʱ���ڵ�A��F��2=A��D��2ʱ���۵�D��F��2=A��D��2ʱ�г����̼��ɽ�����⡣
t����ó�A�䣬D������꣬�ɵ�A��F2����D��F��2��A��D��2�ij��ȣ�Ȼ����������ٵ�A��F2=D��F��2ʱ���ڵ�A��F��2=A��D��2ʱ���۵�D��F��2=A��D��2ʱ�г����̼��ɽ�����⡣
�����㾫����������Ĺؼ�������������Գ�ͼ�ε����֪ʶ�����ջ��Գ���ͼ�εķ������ٱ���ؼ������������ԳƵ���������ߣ��Լ������������ε����ʵ����⣬�˽��Ӧ����ȣ���Ӧ�߳ɱ��������������ν������������Σ�

 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
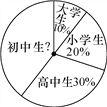
��ӡ�Ļ���ʱ����ϵ�д�����Ŀ���ڶ��������·����һ��Ѳ��ͤA��Ѳ��Ա�״Ӹ�ͤA������13km/h�ٶ���������Ѳ�ߣ�����涨��Ѳ��Ϊ��������Ѳ��Ϊ����Ѳ�������¼���£�����λ��ǧ�ף�
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | ���ߴ� |
4 | -5 | 3 | -4 | -3 | 6 | -1 |
��1��������ν���ʱ��λ�ã��ڸ�ͤA�Ķ��������ߣ������Զ����
��2���ڵڼ��ν���ʱ���ͤA��Զ������A��Զ��
��3��Ѳ�߹������������߶Խ�������һֱ�������ڸ�ͤA���ҽ���ͨ�������ڼ�Ѳ�߹����У������ҵı���ͨ��ʱ��������Сʱ��
����Ŀ��ѧУ���Ӽ�����λѡ����ѡ��һλѡ�ִ���ѧУ�μ����ڵ����ĺ�����д������ѧУ����λѡ�ִӱ����������Ķ����⡢�ۺ����ʺͺ�����д�ĸ��������˲��ԣ����Ǹ��Եijɼ����ٷ��ƣ������
ѡ�� | �������� | �Ķ����� | �ۺ����� | ������д |
�� | 85 | 78 | 85 | 73 |
�� | 73 | 80 | 82 | 83 |
��1���ɱ��гɼ�����ü�ƽ���ɼ�Ϊ80.25��������ҵ�ƽ���ɼ��������ǵ���һ�ɼ�����Ӧѡ��˭��
��2����������������Ķ����⡢�ۺ����ʺͺ�����д�ֱ�������2��1��3��4��Ȩ����ֱ��������ѡ�ֵ�ƽ���ɼ��������ǵ���һ�ɼ�����Ӧѡ��˭��