��Ŀ����
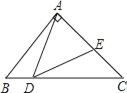
����Ŀ����ͼ����ABC�У���BAC=90�㣬AB=AC=1����D��BC��һ�����㣨����B��C�غϣ�����AC��ȡE�㣬ʹ��ADE=45�㣮
��1�����ж���ABD����DCE�Ƿ����Ʋ�˵�����ɣ�
��2����BD=x��AE=y����y����x�ĺ�����ϵʽ����ָ������D��BC���˶�������B��C�غϣ�ʱ��AE�Ƿ������Сֵ�������ڣ������Сֵ���������ڣ�˵�����ɣ�
��3������ADE�ǵ���������ʱ����AE�ij���
���𰸡���1����ABD����DCE���ƣ����ɼ�����2��x=![]() ʱ��y����Сֵ����СֵΪ
ʱ��y����Сֵ����СֵΪ![]() ����3������ADE�ǵ���������ʱ��AE�ij�Ϊ2��
����3������ADE�ǵ���������ʱ��AE�ij�Ϊ2��![]() ��
��![]()
��������
��1�����ݵ���ֱ�������ε����ʼ��������ڽ�����ǵĹ�ϵ����֤��ABD�ס�DCE��
��2���ɡ�ABD�ס�DCE����Ӧ�߳ɱ���������ֱ�������ε����ʿ����y��x�ĺ�����ϵʽ�����ݺ���ͼ��Ķ���������������Сֵ��
��3������ADE�ǵ���������ʱ����Ϊ�����ε����͵ײ���ȷ������Ӧ��AD=DE��AE=DE��AD=AE����������ۣ�
�⣺��1����ABD����DCE����
�ߡ�BAC=90�㣬AB=AC
���B=��C=��ADE=45��
�ߡ�ADC=��B+��BAD=��ADE+��CDE
���BAD=��CDE
���ABD�ס�DCE��
��2���ɣ�1������ABD�ס�DCE
��![]() ��
��
�ߡ�BAC=90�㣬AB=AC=1��
��BC=![]() ��DC=
��DC=![]() ��x��EC=1��y
��x��EC=1��y
��![]() ��y=x2��
��y=x2��![]() x+1=��x��
x+1=��x��![]() ��2+
��2+![]() ��
��
��x=![]() ʱ��y����Сֵ����СֵΪ
ʱ��y����Сֵ����СֵΪ![]() ��
��
��3����AD=DEʱ����ABD�ա�CDE��
��BD=CE��
��x=1��y����![]() x��x2=x��
x��x2=x��
��x��0��
��x=![]() ��1
��1
��AE=1��x=2��![]() ��
��
��AE=DEʱ��DE��AC����ʱD��BC�е㣬EҲ��AC���е㣬
���ԣ�AE=![]() ��
��
��AD=AEʱ����DAE=90�㣬D��B�غϣ��������⣻
���ϣ�����ADE�ǵ���������ʱ��AE�ij�Ϊ2��![]() ��
��![]() ��
��

����Ŀ��Сӱ��С����λͬѧ��ѧϰ��������ʱ����Ͷ�����ӣ��ʵؾ��ȵ������壩ʵ�飬���ǹ�����![]() ��ʵ�飬ʵ��Ľ�����£�
��ʵ�飬ʵ��Ľ�����£�
���ϵĵ��� |
|
|
|
|
|
|
���ֵĴ��� |
|
|
|
|
|
|
![]() ������
������![]() �㳯������Ƶ�ʺ���
�㳯������Ƶ�ʺ���![]() �㳯������Ƶ�ʣ�
�㳯������Ƶ�ʣ�
![]() Сӱ˵��������ʵ�飬һ��ʵ���г���
Сӱ˵��������ʵ�飬һ��ʵ���г���![]() �㳯�ϵĸ����������С��˵�������Ͷ��
�㳯�ϵĸ����������С��˵�������Ͷ��![]() �Σ���ô����
�Σ���ô����![]() �㳯�ϵĴ���������
�㳯�ϵĴ���������![]() �Σ���Сӱ��С���˵����ȷ��Ϊʲô��
�Σ���Сӱ��С���˵����ȷ��Ϊʲô��
![]() Сӱ��С���Ͷ��һö���ӣ����б�����״ͼ�ķ��������ö���ӳ��ϵĵ���֮��Ϊ
Сӱ��С���Ͷ��һö���ӣ����б�����״ͼ�ķ��������ö���ӳ��ϵĵ���֮��Ϊ![]() �ı����ĸ��ʣ�
�ı����ĸ��ʣ�
����Ŀ����7�֣�ij��ѧ1000��ѧ���μ���������֪ʶ��������Ϊ���˽Ȿ�ξ����ɼ���������г�ȡ�˲���ѧ���ijɼ����÷�ȡ����������Ϊ100�֣���Ϊ��������ͳ�ƣ�����������ͼƵ���ֲ�����Ƶ���ֲ�ֱ��ͼ���������Ҿֲ�����������������ʾ����������ݣ��������������⣺
�ɼ����� | Ƶ�� | Ƶ�� |
50��x��60 | 8 | 0.16 |
60��x��70 | 12 | a |
70��x��80 | �� | 0.5 |
80��x��90 | 3 | 0.06 |
90��x��100 | b | c |
�ϼ� | �� | 1 |
��1��д��a��b��c��ֵ��
��2���������1000��ѧ�����ж����˵ľ����ɼ�������70�֣�
��3����ѡȡ�������У��Ӿ����ɼ���80�����ϣ���80�֣���ͬѧ�������ȡ����ͬѧ�μӻ���֪ʶ�������������ȡ��2��ͬѧ����ͬһ��ĸ��ʣ�