题目内容
【题目】如图，已知平行四边形ABCD中，对角线AC，BD交于点O，E是BD延长线上的点，且△ACE是等边三角形．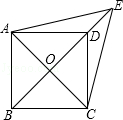 
（1）求证：四边形ABCD是菱形；
（2）若∠AED=2∠EAD，求证：四边形ABCD是正方形．
【答案】
（1）证明：∵四边形ABCD是平行四边形，
∴AO=CO．
又∵△ACE是等边三角形，
∴EO⊥AC（三线合一），即AC⊥BD，
∴四边形ABCD是菱形（对角线互相垂直的平行四边形是菱形）．
（2）∵四边形ABCD是平行四边形，
∴AO=CO．
又∵△ACE是等边三角形，
∴EO平分∠AEC（三线合一），
∴∠AED= 
∠AEC= ×60°=30°，
又∵∠AED=2∠EAD
∴∠EAD=15°，
∴∠ADO=∠DAE+∠DEA=15°+30°=45°（三角形的一个外角等于和它外角不相邻的两内角之和），
∵四边形ABCD是菱形，
∴∠ADC=2∠ADO=90°，
∴平行四边形ABCD是正方形．
【解析】（1）根据对角线互相垂直的平行四边形是菱形．由题意易得△AOE≌△COE，∴∠AOE=∠COE=90°，∴BE⊥AC，∴四边形ABCD是菱形；（2）根据有一个角是90°的菱形是正方形．由题意易得∠ADO=∠DAE+∠DEA=15°+30°=45°，∵四边形ABCD是菱形，∴∠ADC=2∠ADO=90°，∴四边形ABCD是正方形．
练习册系列答案
相关题目
