题目内容
【题目】探究:
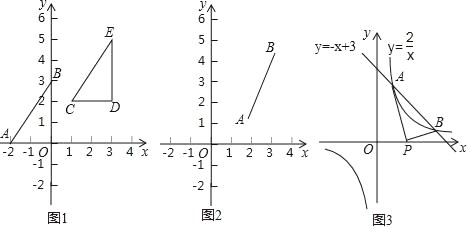
(1)图1中,已知线段AB,A(﹣2,0),B(0,3),则线段AO的长为2,BO的长为3,所以线段AB的长为;把Rt△AOB向右平移3个单位,再向上平移2个单位,得到Rt△CDE.
则Rt△CDE的顶点坐标分别为C(1,2),D(3,2),E(3,5);此时线段CD的长为 ,DE的长为 ,所以线段CE的长为 .
(2)在图2中,已知线段AB的端点坐标为A(a,b),B(c,d),求出图中AB的长AB= (用含a,b,c,d的代数式表示,写出推导过程);
归纳:无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(a,b),B(c,d)时,线段AB的长为AB= .(不必证明)
(3)运用 在图3中,一次函数y=﹣x+3与反比例函数y=![]() 的图象交点为A,B.
的图象交点为A,B.
①求出交点A、B的坐标;
②线段AB的长;
③点P是x轴上动点,求PA+PB的最小值.
【答案】(1) 2;3;![]() ; (2)
; (2)![]() ; (3) ①点A的坐标为(1,2),点B的坐标为(2,1);②
; (3) ①点A的坐标为(1,2),点B的坐标为(2,1);②![]() ;③
;③![]() .
.

练习册系列答案
相关题目