Question

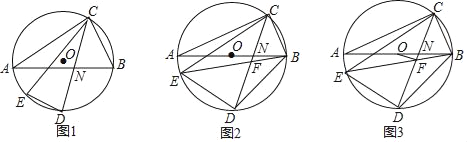
【题目】如图，抛物线y=-(x+k)(x-5)交x轴于点A、B（A左B右），交y轴交于点C，BD⊥AC垂足为D，BD与OC交于点E，且CE=4OE.

⑴如图1，求抛物线的解析式；

⑵如图2，点M为抛物线的顶点,MH⊥x轴,垂足为H,点P为第一象限MH右侧抛物线上一点,PN⊥x轴于点N,PA交MH于点F,FG⊥PN于点G,求tan∠GBN的值；

⑶如图3，在⑵的条件下，过点P作BG的平行线交直线BC于点S，点T为直线PS上一点，TC交抛物线于点Q，若CQ=QT，TS=，求点P的坐标.

Answer 1

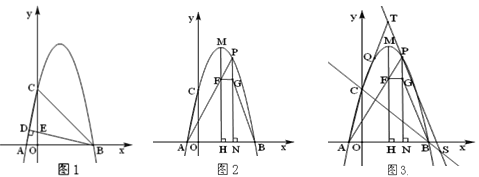
【答案】（1）y=-x2+4x+5；（2）3；（3）P1(3,8),P2(4,5)

【解析】

（1）通过证明△OCA≌△OBE得OC=OB,从而求出k的值，故可得解.

(2) 由y=-x2+4x+5=-（x-2）2+9知对称轴x=2,AH=3. 设P(m,-m2+4m+5)，得tan∠PAN==，由FH=3(5-m)=GN,BN=5-m得tan∠GBN=3；

（3）设Q（t,-t2+4t+5），T(x,y)，由QC=QT得T(2t,-2t2+8t-5)；过点T、S分别作x轴、y轴的平行线，相较于点K，易求TK=4,KS=12，得S(2t+4,-2t2+8t-7)，设直线BC解析式为y=k1x+b,得y=-x+5，作SL⊥PN,tan∠PSL=tan∠1=3，设P（m,-m2+4m+5）则PL=3LS,求得m1=3,m2=4，得P1(3,8),P2(4,5).

(1)令y=0,则x=5,x=-k

∴A(-k,0),B(5,0),C(0,5k)；

∴OC=5k,OA=k,

∵OC=5OE,

∴OE=k=OA,

∴△OCA≌△OBE,

∴OC=OB,

∴5k=5,

∴k=1，

∴抛物线为：y=-x2+4x+5；

（2）y=-x2+4x+5=（x+2）2+1

∴对称轴x=2,AH=3,；

设P(m,-m2+4m+5)

tan∠PAN===5-m=

∴FH=3(5-m)=GN,BN=5-m.；

∴tan∠GBN==3；

(3)设Q（t,-t2+4t+5）,C(0,5),

∵QC=QT，

∴Qx-Cx=Tx-Qx,Qy-Cy=Ty-Qy

设T(x,y)

∴t-0=x-t

-t2+4t+5-5=y- (-t2+4t+5)

∴x=2t,y=-2t2+8t-5,∴T(2t,-2t2+8t-5)；

过点T、S分别作x轴、y轴的平行线，相较于点K

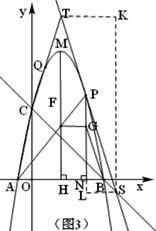
∴∠TKS=90°

∵PS∥BG

∴∠GBN=∠1=∠KTS,∴tan∠KTS=3

∵TS=4,∴TK=4,KS=12

∴S(2t+4,-2t2+8t-7)；

设直线BC解析式为：y=k1x+b,B(5,0),C(0,5)

∴y=-x+5；

∵-2t2+8t-7=2t-4+5,t2-5t+4=0,t1=1,t2=4(舍)，

∴S(6,-1)；

作SL⊥PN,tan∠PSL=tan∠1=3

设P（m,-m2+4m+5）则PL=-m2+4m+5+1=-m2+4m+6,SL=6-m

∴PL=3LS,

∴-m2+4m+6=18-3m,m2-7m+12=0,

∴m1=3,m2=4

∴P1(3,8),P2(4,5)