题目内容
已知:矩形ABCD中AD>AB,O是对角线的交点,过O任作一直线分别交BC、AD于点M、N(如图1).(1)求证:BM=DN;
(2)如图2,四边形AMNE是由四边形CMND沿MN翻折得到的,连接CN,若△CDN的面积与△CMN的面积比为3:5,DC=4,判断
∠ENA+∠ANC是否等于180度?若是说明理由并求四边形ABCE的面
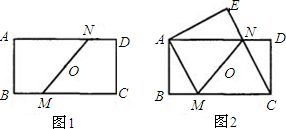 积.若不是说明理由.
积.若不是说明理由.
分析:(1)连AC,根据矩形的性质得到OA=OC,易证△ANO≌△CMO,则AN=MC,即可得到结论;
(2)利用△CDN的面积与△CMN的面积比为3:5得DN:MC=3:5,则DN:AN=3:5,再根据折叠的性质得EN=DN,AE=DC=4,∠E=∠D=90°,在Rt△AEN中利用勾股定理易得AN=5,EN=3,同样可得NC,易证Rt△NEA≌Rt△NDC,则∠ANE=∠DNC,即可得到∠ENA+∠ANC=180°;易得四边形ABCE的面积=四边形ABCD的面积,然后根据矩形的面积公式计算即可.
(2)利用△CDN的面积与△CMN的面积比为3:5得DN:MC=3:5,则DN:AN=3:5,再根据折叠的性质得EN=DN,AE=DC=4,∠E=∠D=90°,在Rt△AEN中利用勾股定理易得AN=5,EN=3,同样可得NC,易证Rt△NEA≌Rt△NDC,则∠ANE=∠DNC,即可得到∠ENA+∠ANC=180°;易得四边形ABCE的面积=四边形ABCD的面积,然后根据矩形的面积公式计算即可.
解答: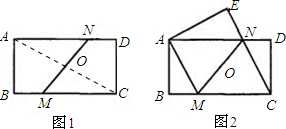 (1)证明:连AC,如图
(1)证明:连AC,如图
∵O是矩形ABCD的对角线的交点,
∴OA=OC,
而AN∥MC,
∴∠OAN=∠OCM,∠ANO=∠OMC,
∴△ANO≌△CMO,
∴AN=MC,
∴BM=DN;
(2)解:∠ENA+∠ANC=180°.理由如下:
∵△CDN的面积与△CMN的面积比为3:5,
∴DN:MC=3:5,
∴DN:AN=3:5,
又∵四边形AMNE是由四边形CMND沿MN翻折得到的,
∴EN=DN,AE=DC=4,∠E=∠D=90°,
在Rt△AEN中,EN:AN=3:5,AE=4,
设EN=3x,则AN=5x,
∴(5x)2=(3x)2+42,解得x=1,
∴AN=5,EN=3,
∴DN=3,
在Rt△DNC中,NC=
=5,
∴Rt△NEA≌Rt△NDC,
∴∠ANE=∠DNC,
∴∠ENA+∠ANC=180°;
∴四边形ABCE的面积=四边形ABCD的面积=4×(3+5)=32.
 (1)证明:连AC,如图
(1)证明:连AC,如图∵O是矩形ABCD的对角线的交点,
∴OA=OC,
而AN∥MC,
∴∠OAN=∠OCM,∠ANO=∠OMC,
∴△ANO≌△CMO,
∴AN=MC,
∴BM=DN;
(2)解:∠ENA+∠ANC=180°.理由如下:
∵△CDN的面积与△CMN的面积比为3:5,
∴DN:MC=3:5,
∴DN:AN=3:5,
又∵四边形AMNE是由四边形CMND沿MN翻折得到的,
∴EN=DN,AE=DC=4,∠E=∠D=90°,
在Rt△AEN中,EN:AN=3:5,AE=4,
设EN=3x,则AN=5x,
∴(5x)2=(3x)2+42,解得x=1,
∴AN=5,EN=3,
∴DN=3,
在Rt△DNC中,NC=
| 32+42 |
∴Rt△NEA≌Rt△NDC,
∴∠ANE=∠DNC,
∴∠ENA+∠ANC=180°;
∴四边形ABCE的面积=四边形ABCD的面积=4×(3+5)=32.
点评:本题考查了折叠的性质:折叠前后两图形全等,即对应角相等,对应线段相等;也考查了勾股定理、矩形的性质以及三角形全等的判定与性质.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 ,tan∠DAE=
,tan∠DAE=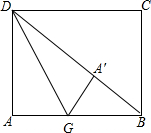 已知在矩形ABCD中.
已知在矩形ABCD中.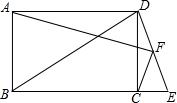 已知,矩形ABCD中,延长BC至E,使BE=BD,F为DE的中点,连结AF、CF.
已知,矩形ABCD中,延长BC至E,使BE=BD,F为DE的中点,连结AF、CF.