题目内容
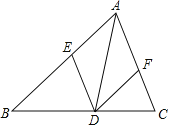
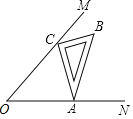
【题目】如图,∠MON=45°,一直角三角尺△ABC的两个顶点C、A分别在OM,ON上移动,若AC=6,则点O到AC距离的最大值为_____.
【答案】3![]() +3
+3
【解析】
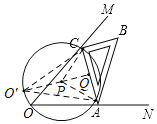
作△AOC的外接圆⊙P,过点P作PQ⊥AC与Q,延长QP⊙P于O',连接PA、PC.当点O在圆周上运动到点O',即点O与O'重合时,点O到AC距离最大,依此列式计算即可求解.
解:如图,作△AOC的外接圆⊙P,过点P作PQ⊥AC与Q,延长QP⊙P于O',连接PA、PC.
当点O在圆周上运动到点O',即点O与O'重合时,点O到AC距离最大.
∵∠MON=45°,
∴∠CO'A=45°,
∴∠CPA=90°,
∵PQ⊥AC,
∴QA=QC=![]() AC=3,
AC=3,
∴PQ=![]() AC=3,
AC=3,
PA=![]() QA=3
QA=3![]() ,
,
OP=AP=3![]() ,
,
∴O'Q=OP+PQ=3![]() +3.
+3.
故答案为3![]() +3.
+3.

练习册系列答案
相关题目