题目内容
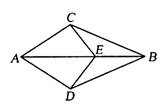
 如图,AD平分∠BAC,AB=AC,连接BD,CD并延长交AC,AB于E,F点,则此图中全等三角形共有
如图,AD平分∠BAC,AB=AC,连接BD,CD并延长交AC,AB于E,F点,则此图中全等三角形共有
- A.2对
- B.3对
- C.4对
- D.5对
C
分析:认真观察图形,确定已知条件在图形上的位置,结合全等三角形的判定方法,由易到难,仔细寻找.
解答:∵AD平分∠BAC,
∴∠BAD=∠CAD,
AB=AC,AD=AD,
∴△ABD≌△ACD,
∴BD=CD,∠B=∠C,∠ADB=∠ADC,
又∠EDB=∠FDC,
∴∠ADE=∠ADF,
∴△AED≌△AFD,△BDE≌△CDF,△ABF≌△ACE.
∴△AED≌△AFD,△ABD≌△ACD,△BDE≌△CDF,△ABF≌△ACE,共4对.
故选C.
点评:本题考查三角形全等的判定方法和全等三角形的性质.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
分析:认真观察图形,确定已知条件在图形上的位置,结合全等三角形的判定方法,由易到难,仔细寻找.
解答:∵AD平分∠BAC,
∴∠BAD=∠CAD,
AB=AC,AD=AD,
∴△ABD≌△ACD,
∴BD=CD,∠B=∠C,∠ADB=∠ADC,
又∠EDB=∠FDC,
∴∠ADE=∠ADF,
∴△AED≌△AFD,△BDE≌△CDF,△ABF≌△ACE.
∴△AED≌△AFD,△ABD≌△ACD,△BDE≌△CDF,△ABF≌△ACE,共4对.
故选C.
点评:本题考查三角形全等的判定方法和全等三角形的性质.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图,AB平分∠CAD,E为AB上一点,若AC=AD,则下列结论错误的是( )
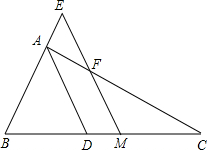
如图,AB平分∠CAD,E为AB上一点,若AC=AD,则下列结论错误的是( )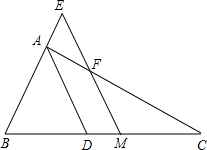 如图,AD为△ABC的角平分线,M为BC的中点,ME∥AD交BA的延长线于E,交AC于F.求证:BE=CF=
如图,AD为△ABC的角平分线,M为BC的中点,ME∥AD交BA的延长线于E,交AC于F.求证:BE=CF=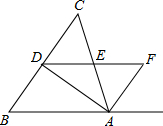 如图,AD是△ABC的角平分线,过点D作直线DF∥BA,交△ABC的外角平分线AF于点F,DF与AC交于点E.
如图,AD是△ABC的角平分线,过点D作直线DF∥BA,交△ABC的外角平分线AF于点F,DF与AC交于点E.