题目内容
A、B、C三点在同一条直线上,M,N分别为AB,BC的中点,且AB=60,BC=40,则MN的长为
- A.30
- B.30或10
- C.50
- D.50或10
D
分析:此题首先要考虑A、B、C三点在直线上的不同位置:点C在线段AB上或点C在线段AB的延长线上.再根据线段中点的概念进行计算.
解答: 解:如图所示,
解:如图所示,
∵M,N分别为AB,BC的中点,
∴BM= AB=30,BN=
AB=30,BN= BC=20.
BC=20.
在图1中,MN=BM-BN=10;在图2中,MN=BM+BN=50.
故选D.
点评:此题的难点在正确考虑三点在直线上的不同位置,掌握线段的中点概念.
分析:此题首先要考虑A、B、C三点在直线上的不同位置:点C在线段AB上或点C在线段AB的延长线上.再根据线段中点的概念进行计算.
解答:
 解:如图所示,
解:如图所示,∵M,N分别为AB,BC的中点,
∴BM=
 AB=30,BN=
AB=30,BN= BC=20.
BC=20.在图1中,MN=BM-BN=10;在图2中,MN=BM+BN=50.
故选D.
点评:此题的难点在正确考虑三点在直线上的不同位置,掌握线段的中点概念.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
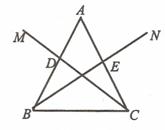 21、已知:如图,在△ABC中,分别延长中线BE、CD至N、M,使EN=EB,DM=DC,求证:点M、A、N三点在同一条直线上.
21、已知:如图,在△ABC中,分别延长中线BE、CD至N、M,使EN=EB,DM=DC,求证:点M、A、N三点在同一条直线上.



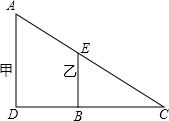 如图,小明站在C处看甲、乙两楼楼顶的点A和E,A、E、C三点在同一直线上,甲乙两楼的底部D、B与C也在同一直线上,测得BC相距20米,DB相距20米,乙楼高BE为15米,则甲楼高(小明身高忽略不计)为
如图,小明站在C处看甲、乙两楼楼顶的点A和E,A、E、C三点在同一直线上,甲乙两楼的底部D、B与C也在同一直线上,测得BC相距20米,DB相距20米,乙楼高BE为15米,则甲楼高(小明身高忽略不计)为 如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.