题目内容
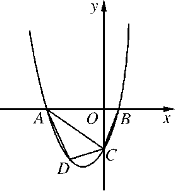
【题目】已知,如图,抛物线![]() >0)与
>0)与![]() 轴交于点C,与
轴交于点C,与![]() 轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
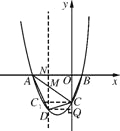
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
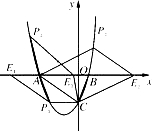
(3)若点E在![]() 轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)、![]() ;(2)、
;(2)、![]() ;(3)、P1(-2,-3),
;(3)、P1(-2,-3),![]() ,
,![]()
【解析】
试题分析:(1)、根据题意得出点B和点C的坐标,然后代入函数解析式求出答案;(2)、首先根据点A和点C的坐标得出直线AC的解析式,然后过点D作DM∥y轴分别交线段AC和x轴于点M,N,设点M的坐标为(m,-m-3),从而得出点D的坐标,求出DM的长度,根据二次函数的性质求出DM的最大值,得出面积的最大值;(3)、①、过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,,将C(0,-3)代入函数解析式求出点P的坐标;②、平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,设出点P的坐标为(x,3),然后代入函数解析式求出点P的坐标.
试题解析:(1)、∵OC=3OB,B(1,0),∴C(0,-3). 把点B,C的坐标代入![]() ,得
,得![]()
∴抛物线的解析式![]()
(2)、由A(-3,0),C(0,-3)得直线AC的解析式为![]() ,
,
如图,过点D作DM∥y轴分别交线段AC和x轴于点M,N.
设M![]() 则D
则D![]() ,
,![]()
∴-1<0,∴当x=![]() 时,DM有最大值
时,DM有最大值![]() ∴S四边形ABCD=S△ABC+S△ACD
∴S四边形ABCD=S△ABC+S△ACD![]()
此时四边形ABCD面积有最大值为![]() .
.
(3)、存在
①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,
此时四边形ACP1E1为平行四边形. ∵C(0,-3),令![]()
∴![]() ,
,![]() .∴P1(-2,-3).
.∴P1(-2,-3).
②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,∵C(0,-3),
∴可令P(x,3),![]() ,得
,得![]() 解得
解得![]() ,
,![]()
此时存在点![]() ,
,![]()
综上所述,存在3个点符合题意,坐标分别是P1(-2,-3),![]()
![]()

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案