Question

（1）如图1，已知AD是△ABC的中线，∠ADC=45°，把△ADC沿AD所在直线对折，点C落在点E的位置（如图1），则∠EBC等于

 

度．
（2）如图2，有一直角三角形纸片，两直角边AC=3，BC=4，将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，求CD的长．

Answer 1

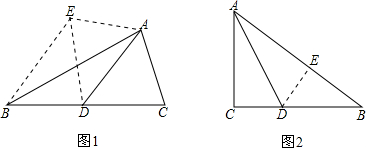
分析：（1）由折叠的性质可知∠EDA=∠ADC=45°，即∠EDC=90°，DC=DE，又AD为△ABC的中线，故BD=DC，即BD=DE，△BDE为等腰直角三角形，可得∠EBC=45°；
（2）由折叠的性质可知DE=CD，AC=AE，∠AED=∠C=90°，在Rt△ABC中，由勾股定理求AB，由BE=AB-AE，设CD=DE=x，则BD=4-x，在Rt△BDE中，由勾股定理求x即可．

解答：解：（1）依题意，得∠EDA=∠ADC=45°，即∠EDC=90°，
又∵DC=DE，AD为△ABC的中线，
∴BD=DC，即BD=DE，△BDE为等腰直角三角形，
∴∠EBC=45°；

（2）令CD=x，则DB=4-x，
由于是直角三角形且是折叠，所以AB=5，AE=AC=3，
DE=x，EB=2，因为∠AED=∠C=90°，
故在Rt△BDE中运用勾股定理得：
（4-x）²=2²+x²，
16-8x=4，解得x=

3

2

，即CD=

3

2

．

点评：本题考查了折叠的性质．折叠前后，对应角相等，对应边相等，结合勾股定理答题．