题目内容

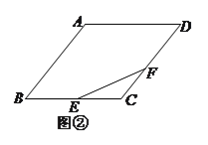
【题目】如图所示，∠1=65°，则∠A+∠B+∠C+∠D+∠E+∠F的度数为___________.

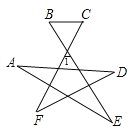
【答案】230°

【解析】

依据三角形内角和定理，即可得到∠B＋∠C＝115°，∠MGH＋∠MHG＝115°，再根据三角形外角性质，即可得出∠A＋∠B＋∠C＋∠D＋∠E＋∠F的度数．

如图所示，

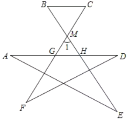
∵∠1＝∠BMC＝65°，

∴∠B＋∠C＝180°65°＝115°，∠MGH＋∠MHG＝115°，

又∵∠MGH是△DFG的外角，∠MHG是△AEH的外角，

∴∠MGH＝∠F＋∠D，∠MHG＝∠A＋∠E，

∴∠F＋∠D＋∠A＋∠E＝∠MGH＋∠MHG＝115°，

∴∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝115°＋115°＝230°，

故答案为：230°．

练习册系列答案
相关题目

【题目】（分）在菱形中， ， ，点是线段上的一个动点．

（）如图①，求的最小值．

（）如图②，若也是边上的一个动点，且，求的最小值．

（）如图③，若，则在菱形内部存在一点，使得点分别到点、点、边的距离之和最小．请你画出这样的点，并求出这个最小值．

【题目】如图，直线： 与轴、轴分别交于点B、C，经过B、C两点的抛物线与轴的另一个交点为A．

（1）求该抛物线的解析式；

（2）若点P在直线下方的抛物线上，过点P作PD∥轴交于点D，PE∥轴交于点E，

求PD+PE的最大值；

（3）设F为直线上的点，以A、B、P、F为顶点的四边形能否构成平行四边形？若能，求出点F的坐标；若不能，请说明理由．

【题目】人民商场准备购进甲、乙两种牛奶进行销售，若甲种牛奶的进价比乙种牛奶的进价每件少5元，其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同．

（1）求甲种牛奶、乙种牛奶的进价分别是多少元？

（2）若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件，该商场甲种牛奶的销售价格为49元，乙种牛奶的销售价格为每件55元，则购进的甲、乙两种牛奶全部售出后，可使销售的总利润（利润=售价﹣进价）等于371元，请通过计算求出该商场购进甲、乙两种牛奶各自多少件？

【题目】已知，如图，抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A，B，此抛物线与x轴的另一个交点为C，抛物线的顶点为D．

（1）求此抛物线的解析式；

（2）若点M为抛物线上一动点，是否存在点M，使△ACM与△ABC的面积相等？若存在，求点M的坐标；若不存在，请说明理由．

（3）在x轴上是否存在点N使△ADN为直角三角形？若存在，确定点N的坐标；若不存在，请说明理由．

【题目】元旦期间，某商场设置了如图所示的幸运转盘，转盘分成4个大小相同的扇形，分别标有数学1，2，3，4，指针的位置固定，转盘可以自由转动，当转动的转盘停止后，其中的某个扇形会停在指针所指的位置（指针指向两个扇形的交线时，当作右边的扇形）．商场规定：凡是参加抽奖的顾客均可转动转盘两次，如果两次转动中指针指缶扇形上的数字之和为8是一等奖，数字之和为7是二等奖，数字之和为6是三等奖，标号之和为其他数字则获得一份纪念品，请分别求出顾客抽中一、二、三等奖的概率．

【题目】综合与探究

如图，在平面直角坐标系xOy中，抛物线W的函数表达式为y=﹣x2+2x+3，抛物线W与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C，它的顶点为D，直线l经过A、C两点．

（1）求点A、B、C、D的坐标．

（2）将直线l向下平移m个单位，对应的直线为l′．

①若直线l′与x轴的正半轴交于点E，与y轴的正半轴交于点F，△AEF的面积为S，求S关于m的函数关系式，并写出自变量m的取值范围；

②求m的值为多少时，S的值最大？最大值为多少？

（3）若将抛物线W也向下平移m单位，再向右平移1个单位，使平移后得到的二次函数图象的顶点P落在△AOC的内部（不包括△AOC的边界），请直接写出m的取值范围．

【题目】已知AB∥DE，∠ABC＝800，∠CDE＝1400.请你探索出一种（只须一种）添加辅助线求出∠BCD度数的方法，并求出∠BCD的度数.

【题目】如图，二次函数y＝ax2＋bx＋c(a≠0)的图象的顶点在第一象限，且过点(0，1)和(－1，0)．下列结论：①ab＜0；②b2＞4a；③0＜a＋b＋c＜2；④0＜b＜1；⑤当x＞－1时，y＞0.其中正确结论的个数是( )

A. 5个 B. 4个 C. 3个 D. 2个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网