题目内容
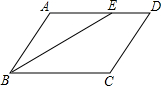 如图,?ABCD中,∠C=108°,BE平分∠ABC,则∠ABE等于( )
如图,?ABCD中,∠C=108°,BE平分∠ABC,则∠ABE等于( )| A、18° | B、36° | C、72° | D、108° |
分析:因为平行四边形对边平行,由两直线平行,同旁内角互补,已知∠C,可求∠ABC,又BE平分∠ABC,故∠ABE=
∠ABC.
| 1 |
| 2 |
解答:解:∵AB∥CD,
∴∠ABC+∠C=180°,
把∠C=108°代入,得∠ABC=180°-108°=72°.
又∵BE平分∠ABC,
∴∠ABE=
∠ABC=
•72°=36°.
故选B.
∴∠ABC+∠C=180°,
把∠C=108°代入,得∠ABC=180°-108°=72°.
又∵BE平分∠ABC,
∴∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题直接通过平行四边形性质的应用,判断出正确的选项,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,?ABCD中,AB⊥AC,AB=1,BC=
如图,?ABCD中,AB⊥AC,AB=1,BC=| 5 |
| A、当旋转角为90°时,四边形ABEF一定为平行四边形 |
| B、在旋转的过程中,线段AF与EC总相等 |
| C、当旋转角为45°时,四边形BEDF一定为菱形 |
| D、当旋转角为45°时,四边形ABEF一定为等腰梯形 |
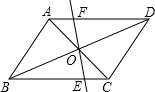
 9、如图,?ABCD中,O为AC、BD的中点,则图中全等的三角形共有( )
9、如图,?ABCD中,O为AC、BD的中点,则图中全等的三角形共有( )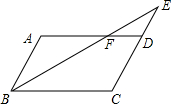 如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=
如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= 已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.
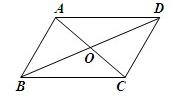
已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F. (1997•浙江)如图,?ABCD中,对角线AC和BD交于点O,过O作OE∥BC交DC于点E,若OE=5cm,则AD的长为
(1997•浙江)如图,?ABCD中,对角线AC和BD交于点O,过O作OE∥BC交DC于点E,若OE=5cm,则AD的长为