��Ŀ����
 �Ķ����ϣ�
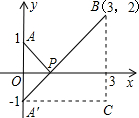
�Ķ����ϣ���ֱ������ϵ�У���֪ƽ����A��x1��y2����B��x1��y2���������꣬��A��B����֮��ľ������
| (x2-x2)2(y2-y1)2 |
����˵������ʽ
| x2+1 |
| (x-3)2+4 |
�⣺
| x2+1 |
| (x-3)2+4 |
| (x-0)2+(0-1)2 |
| (x-3)2+(0-2)2 |
| (x-0)2+(0-1)2 |
| (x-3)2+(0-2)2 |
���A����x��ĶԳƵ�ΪA�䣬��PA=PA�䣬��ˣ���PA+PB����Сֵ��ֻ����PA��+PB����Сֵ������A�䡢B���ֱ�߶ξ�����̣�����PA��+PB����СֵΪ�߶�A��B�ij��ȣ�Ϊ�ˣ�����ֱ��������A��CB����ΪA��C=
3
3
��CB=3
3
������A��B=3
| 2 |
3
����ԭʽ����СֵΪ| 2 |
3
| 2 |
3
��| 2 |
���������Ķ����ϣ�����������⣺
��1�����������գ�
��2������ʽ
| (x-i)2+1 |
| (x-2)2+9 |
��2��3��
��2��3��
�ľ���֮�ͣ�����д��B�����꣩��3�������ʽ
| x2+49 |
| x2-12x+37 |
��������1������B��A����������A��C=3��BC=3���ɹ��ɶ������A��B���ɣ�
��2��
+
=
+
�����ɵó��𰸣�
��3�����
+
=
+
���ó��������ʽ��ֵ���Կ���ƽ��ֱ������ϵ�е�P��x��0�����A��0��7������B��6��1���ľ���֮�ͣ���A����x��ĶԳƵ�ΪA�䣬���A��B���ɣ�
��2��
| (x-i)2+1 |
| (x-2)2+9 |
| (x-1)2+(0-1)2 |
| (x-2)2+(0-3)2 |
��3�����
| x2+49 |
| x2-12x+37 |
| (x-0)2+(0-7)2 |
| (x-6)2+(0-1)2 |
����⣺��1����B��3��2����A�䣨0��-1����
��A��C=3��BC=2-��-1��=3��
�ɹ��ɶ����ã�A��B=
=3
��
��ԭʽ����Сֵ��3
��
�ʴ�Ϊ��3��3��3
��3
��
��2����
+
=
+
��
�����ʽ
+
��ֵ���Կ���ƽ��ֱ������ϵ�е�P��x��0�����A��1��1������B��2��3���ľ���֮�ͣ�
�ʴ�Ϊ����2��3����
��3��
+
=
+
=
+
��
���������ʽ��ֵ���Կ���ƽ��ֱ������ϵ�е�P��x��0�����A��0��7������B��6��1���ľ���֮�ͣ�
��ͼ��ʾ��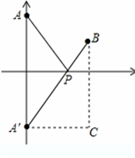
����A����x��ĶԳƵ�ΪA�䣬��PA=PA�䣬
��PA+PB����Сֵ��ֻ����PA��+PB����Сֵ������A�䡢B��ľ�����̣�
��PA��+PB����СֵΪ�߶�A��B�ij��ȣ�
��A��0��7����B��6��1����
��A�䣬-7����
��A��C=6��BC=8��
�ɹ��ɶ����ã�A��B=
=10��
������ʽ
+
����Сֵ��10��
��A��C=3��BC=2-��-1��=3��
�ɹ��ɶ����ã�A��B=
| 32+32 |
| 2 |
��ԭʽ����Сֵ��3
| 2 |
�ʴ�Ϊ��3��3��3
| 2 |
| 2 |
��2����
| (x-i)2+1 |
| (x-2)2+9 |
| (x-1)2+(0-1)2 |
| (x-2)2+(0-3)2 |
�����ʽ
| (x-i)2+1 |
| (x-2)2+9 |
�ʴ�Ϊ����2��3����
��3��
| x2+49 |
| x2-12x+37 |
| x2+72 |
| (x-6)2+12 |
| (x-0)2+(0-7)2 |
| (x-6)2+(0-1)2 |
���������ʽ��ֵ���Կ���ƽ��ֱ������ϵ�е�P��x��0�����A��0��7������B��6��1���ľ���֮�ͣ�
��ͼ��ʾ��

����A����x��ĶԳƵ�ΪA�䣬��PA=PA�䣬
��PA+PB����Сֵ��ֻ����PA��+PB����Сֵ������A�䡢B��ľ�����̣�
��PA��+PB����СֵΪ�߶�A��B�ij��ȣ�
��A��0��7����B��6��1����
��A�䣬-7����
��A��C=6��BC=8��
�ɹ��ɶ����ã�A��B=
| 62+82 |
������ʽ
| x2+49 |
| x2-12x+37 |
���������⿼���˹��ɶ�������Գ�-���·�������Ӧ�ã���Ҫ����ѧ�����Ķ����������ͼ�����������

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 Ϊ��
Ϊ��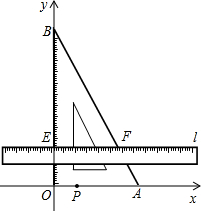 �Ķ����ϣ���ֱ���������У�30�����Ե�ֱ�DZ���б�ߵ�һ�룮
�Ķ����ϣ���ֱ���������У�30�����Ե�ֱ�DZ���б�ߵ�һ�룮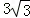 ��������P��A�㿪ʼ������AO��OB��BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1��
��������P��A�㿪ʼ������AO��OB��BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1��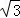 ��2����λ����/�룩��һֱ�ߵ��ϱ�Եl��x���λ�ÿ�ʼ��
��2����λ����/�룩��һֱ�ߵ��ϱ�Եl��x���λ�ÿ�ʼ�� 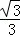 ����λ����/�룩���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F����q�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P������AO��OB��BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶���
����λ����/�룩���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F����q�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P������AO��OB��BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶���
 ��������P��A�㿪ʼ������AO-OB-BA�˶�����P��AO��OB��BA���˶����ٶȷֱ�Ϊ1��
��������P��A�㿪ʼ������AO-OB-BA�˶�����P��AO��OB��BA���˶����ٶȷֱ�Ϊ1�� ��2����λ����/�룩��һֱ�ߵ��ϱ�Եl��x���λ�ÿ�ʼ��
��2����λ����/�룩��һֱ�ߵ��ϱ�Եl��x���λ�ÿ�ʼ�� ����λ����/�룩���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F����q�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P������AO-OB-BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶���
����λ����/�룩���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F����q�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P������AO-OB-BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶���