题目内容

结合所给的阅读材料，求解问题．
材料：在直角坐标系中，如果有两点A（a，b），B（a，0），那么称点B是点A在x轴上的射影．
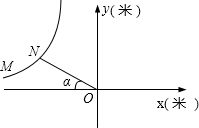
问题：如图，测得飞机的运动曲线是双曲线，飞机在点M的坐标为（-4500
3
，1125），炮弹在点O处沿α角向飞机射击，在点N处命中目标，此时点N在x轴上的射影坐标精英家教网为（-2250
3
，0），已知α=30°，炮弹飞行速度为750米/秒．
问：炮弹从发射到击中目标用了多少时间？
分析：作NA⊥x轴于点A，根据点N的射影可以求得OA的长，然后根据α=30°求得ON的长后除以炮弹的速度即可得到所用时间．
解答：解：作NA⊥x轴于点A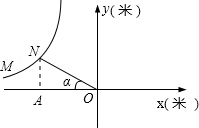，精英家教网
∵点N在x轴上的射影坐标为（-2250
3
，0），
∴OA=2250
3
，
∵α=30°，
∴ON=OA÷cosα=2250
3
÷
3
2
=4500米，
∵炮弹飞行速度为750米/秒．
∴4500÷750=6秒，
∴炮弹从发射到击中目标用了6秒．
点评：本题考查了反比例函数的应用，解题的关键是正确的理解坐标系中点在x轴上的射影．
练习册系列答案
相关题目
（32分）古今中外，无数的仁人志士强调关注民生，维护人性尊严，提倡宽容，反对暴力，主张自由平等和自我价值的体现。阅读下列材料：
材料一  从此观之，财之与势，固英雄之所必资，而大圣人之所必用也，何可言无也?吾故曰，虽大圣人不能无势利之心。则知势利之心，亦吾人秉赋之“自然”矣。    
——《李氏（贽）文集》卷一
材料二  对于全国人民之食衣住行四大需要，政府当与人民协力，共谋农业之发展，以足民食；共谋织造之发展，以裕民衣；建筑大计划之各式屋舍，以乐民居；修治道路、运河，以利民行……每县开创自治之时，必须先规定全县私有土地之价，其法由地主自报之，地方政府则照价征税，并可随照价收买……土地之岁收，地价之增益，公地之生产，山林川泽之息，矿产水力之利，皆为地方政府之所有，而用以经营地方人民之事业……各县之天然富源及大规模之工商事业，本县之资力不能发展与兴办，而须外资（指外地资本）乃能经营者，当由中央政府为之协助。  ——孙中山《国民政府建国大纲》
材料三  我们不要四面出击。四面出击，全国紧张，很不好。绝不可树敌太多，必须在一个方面有所让步，有所缓和，……我们一定要做好工作，使工人、农民、小手工业者都拥护我们，使民族资产阶级和知识分子中的绝大多数不反对我们。 ——毛泽东《不要四面出击》
材料四  社会给予他们的委托以及上帝和自然法对各种政体的国家机关的权力所定的界限：第一，它们应当以正式公布的固定法律进行统治，这些法律不论贫富、不论宫廷权贵和乡村农夫都一视同仁，不因特殊情况而有所改变。第二，这些法律知识为了人民的福利这一最终目的，此外不应再有其他目的。第三，未经人民自己或其代表同意，决不能对人民的财产课税。第四，（立法权和执行权该由不同的人员行使，法官应该独立。）立法机关既不应该也不能把制定法律的权力转让给其他任何人，也不能把它置于并非人民安排的其他任何地方。   ——洛克《政府论》
（1）材料一所述思想主张产生的社会根源是什么?（4分）
（2）依据材料二，概括孙中山建国大纲的主要主张（不得摘抄原文）。（6分）
（3）结合所学知识，概括指出20世纪30年代初期，我们是怎样使农民、小手工业者都拥护我们的?建国初期，我们又是怎样使民族资产阶级中的大多数不反对我们的（12分）
（4）依据材料四，概括指出洛克的主要思想主张。（10分）

二战期间，德日法西斯的疯狂侵略和血腥屠杀给世界人民带来了深重灾难。回顾那段痛苦的日子，我们应该以史为鉴，面向未来，警惕个别国家右翼势力的危险举动和恐怖主义活动。阅读材料，回答问题。
材料一 二战期间，纳粹德国在波兰建立了奥斯威辛集中营，共有110万人在这里被杀害。1945年1月27日，苏联红军解放了该集中营。在瑞典、英国、波兰等许多国家，1月27日已经成为大屠杀遇害者的法定纪念日。1996年，德国也将每年的这一天定为“纳粹受害者纪念日”，告诫人们要永远记住这段惨痛的历史．

图1 一群犹太人正被赶往奥斯维辛集中营   图2一名女子在英国爱丁堡点燃蜡烛，纪念
奥斯维辛集中营解放56周年。
材料二 《联合固宪章))第一次庄严宣布：“欲免后世再遭近代人类身历不堪言之战祸，重申基本人权、人格尊严与价值，以及男女与大小各国平等权利之信念”。经历了法西斯的浩劫和战火的洗礼，战后人类的理性进一步得到弘扬，民主、人权与和平的思想深入人心。
请回答：
(1)指出材料一反映的法西斯反人类政策。1979年联合国教科文组织将奥斯威辛集中营列世界文化遗产名录，对此谈谈你的看法。
(2)据材料二并结合所学知识指出，二战后国际社会为防止战争悲剧重演进行了哪些努力?效果如何?

先阅读材料，再填空解答：

学校为了解九年级学生体育测试情况，以九年级（1）班学生的体育测试成绩为样本，按四个等级进行统计，并将统计结果绘制成如下的统计图，

 

 

 

 

 

 

 

 

 

 

 

请你结合图中所给信息解答下列问题：（说明：A级：90分~100分；B级：75分~89分；C级：60分~74分；D级：60分以下）

 （1）请把条形统计图补充完整；

（2）样本中D级的学生人数占全班学生人数的百分比是             ；

（3）扇形统计图中B级所在的扇形的圆心角度数是             ；

（4）若该校九年级有1000名学生，请你用此样本估计体育测试中A级和B级的学生人数约为                人．

 

结合所给的阅读材料，求解问题．
材料：在直角坐标系中，如果有两点A（a，b），B（a，0），那么称点B是点A在x轴上的射影．
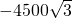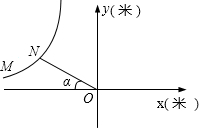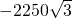问题：如图，测得飞机的运动曲线是双曲线，飞机在点M的坐标为（数学公式，1125），炮弹在点O处沿α角向飞机射击，在点N处命中目标，此时点N在x轴上的射影坐标为（数学公式，0），已知α=30°，炮弹飞行速度为750米/秒．
问：炮弹从发射到击中目标用了多少时间？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网