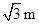题目内容
如图,四边形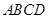 ,
,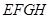 ,
,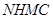 都是正方形,边长分别为
都是正方形,边长分别为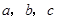 ;
;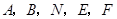 五点在同一直线上,则
五点在同一直线上,则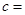 (用含有
(用含有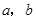 的代数式表示).
的代数式表示).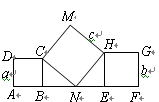
 ,
, ,
, 都是正方形,边长分别为
都是正方形,边长分别为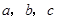 ;
;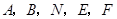 五点在同一直线上,则
五点在同一直线上,则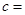 (用含有
(用含有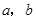 的代数式表示).
的代数式表示).
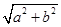
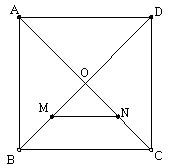
解:由三个正方形如图的摆放,因为四边形ABCD、EFGH、NHMC都是正方形,所以∠CNB+∠ENH=90°,
又因为∠CNB+∠NCB=90°,∠ENH+∠EHN=90°,所以∠CNB=∠EHN,∠NCB=∠ENH
又因为CN=NH,∴△CBN≌△NEH,
所以HE=BN,故在Rt△CBN中,BC2+BN2=CN2,
又已知三个正方形的边长分别为a,b,c,则有a2+b2=c2,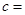
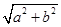 .
.
又因为∠CNB+∠NCB=90°,∠ENH+∠EHN=90°,所以∠CNB=∠EHN,∠NCB=∠ENH
又因为CN=NH,∴△CBN≌△NEH,
所以HE=BN,故在Rt△CBN中,BC2+BN2=CN2,
又已知三个正方形的边长分别为a,b,c,则有a2+b2=c2,
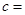
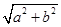 .
.
练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
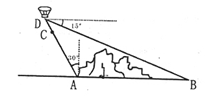
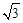 ≈1.732,结果保留三个有效数字).
≈1.732,结果保留三个有效数字).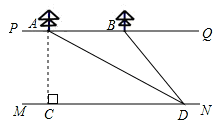
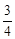 ,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m.求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m.求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)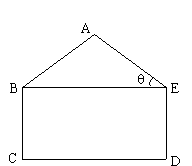
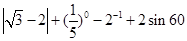 °.
°.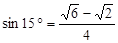 ,
,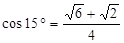 ,
,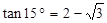 ,
,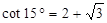 )。
)。

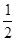 B.
B.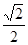 C.
C.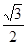 D.1
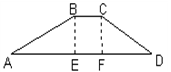
D.1 的斜坡上两树间的水平距离
的斜坡上两树间的水平距离 为
为 ,则两树间的坡面距离
,则两树间的坡面距离 为( )
为( )