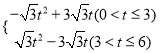��Ŀ����
����Ŀ����ͼ������������y=![]() ��x��0����һ�κ���y=kx+6
��x��0����һ�κ���y=kx+6![]() ���ڵ�C��2��4
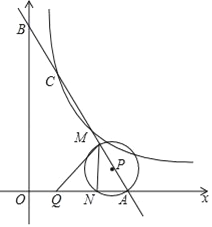
���ڵ�C��2��4![]() ����һ�κ���ͼ������������ֱ��ڵ�A�͵�B������P�ӵ�A��������AB��ÿ��1����λ���ȵ��ٶ����B�˶���ͬʱ������Q�ӵ�O��������OA����ͬ���ٶ����A�˶����˶�ʱ��Ϊt�루0��t��6�����Ե�PΪԲ�ģ�PAΪ�뾶�ġ�P��AB���ڵ�M����OA���ڵ�N������MN��MQ��
����һ�κ���ͼ������������ֱ��ڵ�A�͵�B������P�ӵ�A��������AB��ÿ��1����λ���ȵ��ٶ����B�˶���ͬʱ������Q�ӵ�O��������OA����ͬ���ٶ����A�˶����˶�ʱ��Ϊt�루0��t��6�����Ե�PΪԲ�ģ�PAΪ�뾶�ġ�P��AB���ڵ�M����OA���ڵ�N������MN��MQ��
��1����m��k��ֵ��
��2����tΪ��ֵʱ����Q���N�غϣ�
��3������MNQ�����ΪS������S��t�ĺ�����ϵʽ��
���𰸡���1��m��8![]() ��k����
��k����![]() ����2��t=3����3��S=
����2��t=3����3��S=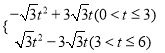
�������������������1�����ô���ϵ����ֱ�����m��k��
��2�������AB�������жϳ���MAN�ס�BAO�����ñ���ʽ�ó�AN��MN�����ɵó�ON������ON=OQ����������⼴�ɣ�
��3��������������������ε������ʽ���ɵó����ۣ�
�⣺��1����C��2��4![]() ������y=
������y=![]() �еã�m=8
�еã�m=8![]()
����2��3![]() ������y=kx+6
������y=kx+6![]() �еã�2k+6=4
�еã�2k+6=4![]()
��k=��![]()
��2���ɣ�1��֪��k=��![]() ��
��
��ֱ��AB�Ľ���ʽΪy=��![]() x+6
x+6![]() ��
��
��A��6��0����B��0��6![]() ����
����
��AB=12
��AM��ֱ��
���ANM=90����
���ANM=��AOB
�֡ߡ�MAN=��BAO��
���MAN�ס�BAO��
��![]()
��OQ=AP=t��AM=2AP=2t��OA=6��OB=6![]() ��AB=12
��AB=12
��![]()
��AN=t��MN=![]() t
t
��ON=OA��AN=6��t
�ߵ�Q���N�غ�
��ON=OQ
��6��t=t
��t=3
��3���ٵ�0��t��3ʱ��QN=OA��OQ��AN=6��2t
��S=![]() QNMN=
QNMN=![]() ��6��2t��
��6��2t��![]() t=��
t=��![]() t2+3
t2+3![]() t
t
�ڵ�3��t��6ʱ��QN=OQ+NA��OA=t+t��6=2t��6
��S=![]() QNMN=
QNMN=![]() ��2t��6��
��2t��6��![]() t=
t=![]() t2��3
t2��3![]() t��
t��
����S=