Question

【题目】如图，在平面直角坐标系中，直线上一点，为轴上一点，连接，线段绕点逆时针旋转90°至线段，过点作直线轴，垂足为，直线与直线交于点，且，连接，直线与直线交于点，则点的坐标为（______）

Answer 1

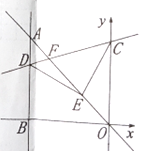
【答案】（，）．

【解析】

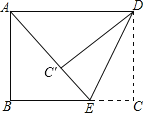
过E作MN⊥y轴，交y轴于M，交AB于N，过D作DH⊥y轴，交y轴于H，∠CME＝∠DNE＝∠CED＝90°，求出∠MCE＝∠DEN，证△MCE≌△NED，推出DN＝EM，EN＝CM，设AD＝a，求出DN＝2a1，得出2a1＝1，求出a＝1，得出D的坐标，在Rt△DNE中，由勾股定理求出EC＝ED＝，在Rt△MCE中，由勾股定理求出CM＝2，得出C的坐标，设直线CD的解析式是y＝kx＋3，把D（-3，2）代入求出直线CD的解析式，解由两函数解析式组成的方程组，求出方程组的解即可．

解：过E作MN⊥y轴，交y轴于M，交AB于N，过D作DH⊥y轴，交y轴于H，

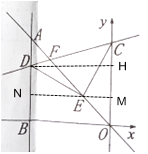
∠CME＝∠DNE＝∠CED＝90°，

∴∠MCE＋∠CEM＝90°，∠MEC＋∠DEN＝90°，

∴∠MCE＝∠DEN，

∵E（-1，1），

∴OM＝BN＝1，EM＝1，

在△MCE和△NED中，

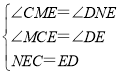
∴△MCE≌△NED（AAS），

∴DN＝EM，EN＝CM，

∵BD＝2AD，

∴设AD＝a，BD＝2a，

∵E（1，1），

∴BN＝2a1，

则2a1＝1，

a＝1，即BD＝2．

∵直线y＝-x，

∴AB＝OB＝3，

在Rt△DNE中，由勾股定理得：EC＝ED＝，

在Rt△MCE中，由勾股定理得：CM＝

则C的坐标是（0，3），

设直线CD的解析式是y＝kx＋3，

把D（-3，2）代入得：k＝，

即直线CD的解析式是y＝x＋3，

即方程组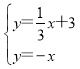

得：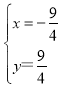

即F的坐标是（，）．

故答案为：（，）．