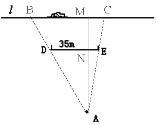
题目内容
【题目】如图,已知![]() ,直线
,直线![]() 分别与
分别与![]() 、
、![]() 交于点
交于点![]() 、点
、点![]() .
.
(1)如图1,当点![]() 在线段
在线段![]() 上,若
上,若![]() ,
,![]() ,则
,则![]() __________°;
__________°;

(2)如图2,当点![]() 在线段
在线段![]() 的延长线上,
的延长线上,![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() 、
、![]() 、
、![]() 之间满足怎样的关系,请证明你的结论;
之间满足怎样的关系,请证明你的结论;

(3)如图3,在(2)的条件下,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,射线
,射线![]() 将
将![]() 分成
分成![]() ,且与
,且与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)70;(2)∠EAF=∠AED+∠EDG.理由见解析;(3)∠EKD=142°.
【解析】
(1)延长DE交AB于H,依据平行线的性质,可得∠D=∠AHE=40°,再根据∠AED是△AEH的外角,即可得到∠AED=∠A+∠AHE=30°+40°=70°;
(2)依据AB∥CD,可得∠EAF=∠EHC,再根据∠EHC是△DEH的外角,即可得到∠EHG=∠AED+∠EDG,即∠EAF=∠AED+∠EDG;
(3)设∠EAI=α,则∠BAE=3α,进而得出∠EDK=α-2°,依据∠EHC=∠EAF=∠AED+∠EDG,可得3α=22°+2α-4°,求得∠EDK=16°,即可得出∠EKD的度数.
解:(1)如图1,延长DE交AB于H,
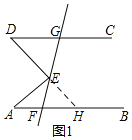
∵AB∥CD,
∴∠D=∠AHE=30°,
∵∠AED是△AEH的外角,
∴∠AED=∠A+∠AHE=40°+30°=70°,
故答案为:70;
(2)∠EAF=∠AED+∠EDG.
理由:如图2,
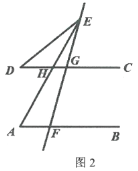
∵AB∥CD,
∴∠EAF=∠EHC,
∵∠EHC是△DEH的外角,
∴∠EHG=∠AED+∠EDG,
∴∠EAF=∠AED+∠EDG;
(3)如图3,
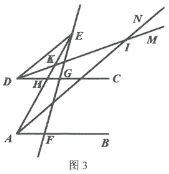
∵∠EAI:∠BAI=1:2,
∴设∠EAI=α,则∠BAE=3α,
∵∠AED=22°,∠I=20°,∠DKE=∠AKI,
又∵∠EDK+∠DKE+∠DEK=180°,∠KAI+∠KIA+∠AKI=180°,
∴∠EDK=α-2°,
∵DI平分∠EDC,
∴∠CDE=2∠EDK=2α-4°,
∵AB∥CD,
∴∠EHC=∠EAF=∠AED+∠EDG,
即3α=22°+2α-4°,
解得α=18°,
∴∠EDK=16°,
∴在△DKE中,∠EKD=180°-16°-22°=142°.